목차
2023학년도 2학기 충남대학교 조은선 교수님의 컴파일러개론 수업 정리자료입니다.
📁 Type Checking
수행 중 변수가 가지는 값에 대한 기술을 타입(Type)이라고 한다.
예를 들어 int x라고 하면, x가 integer값 범위에 들어가는 값을 가지게 된다. 라는 뜻
타입 오류라는건 값을 부적절하게 사용하거나, 값의 범위를 벗어남.
타입 오류가 없다는건 타입 안정성이 있다고 표현할 수 있으며, 타입 안정성을 보장하는 방법은 다음과 같다.
- 타입을 선언(binding)한다. 선언 방법에는 int x와 같이 명시적인 방법과 x=1과 같이 암묵적인 방법이 있다.
- 타입을 검사(checking)한다. 타입 규칙을 세우고 이에 대해 검사한다.
타입과 관련된 몇가지 개념들을 보자.
1. Static vs. dynamic checking
타입 검사 시점을 말한다. 타입 검사를 컴파일때 하면 static (C), 런타임때 하면 dynamic (Python)
static : 컴파일할 때 수행 전에 타입 검사를 한다.
2. Static vs. dynamic typing
타입 정의 시점을 말한다. 타입이 컴파일 전에 다 주어져야하면 static (C), 런타임때 타입이 정해지면 dynamic (Python)
static : 런타임에 타입을 generation하지 않고, 컴파일할때 모든 struct를 정의되어있어야함.
3. Strong vs. weak typing
언어나 컴파일러가 타입 오류를 엄격하게 방지하면 strong, 타입 오류가 날 수도 있는걸 조금 허용해주면 weak.
4. Sound type systems
모든 타입 오류를 방지하는 타입 규칙들의 집합 및 enforce 시스템
🌱 타입 표현식(Type Expressions)
프로그래밍 언어마다 기본적으로 제공하는 비슷한 타입들이 있음. int, float, char ...
또 대부분의 언어에서 배열, struct, pointer 함수 등을 제공하는데, 이건 기본 타입을 조합하거나 활용해서 만든 것들.
배열 타입은 원소 타입에 각괄호 사용. 어떤 경우에는 크기까지 타입으로 넣어주는 경우가 있음.
– Array types : T[], T[10], T[1..10], T[2][3] • 각 원소 접근, 지정 시 타입 유의
– Structure types : {id1 : T1 , … , idn : Tn} • 필드 접근, 지정 시 타입 유
– Pointer types : T * • 내용 접근, 지정 시 타입 유의
– Function types : T1 T2 … Tn → Treturn • 호출 시 인자와 리턴 값 타입 유의
🌱 타입 규칙
타입 검사를 할 때는 타입 규칙을 기반으로 이 expression이 올바른지 검증한다.
예를 들면 int + float 하면 float가 나온다던지, float f(int x)에 인자로 3을 주면 float 타입 결과를 리턴한다던지.
객체지향언어같은 경우 subtyping까지 이런식으로.
자바같은 경우 명세의 반 이상이 타입 얘기.
이런 규칙을 가지고 타입이 옳은지 판단하는 형식언어를 타입 judgment라고 한다. 어휘분석에서는 정규표현식, 구문분석에서는 CFG를 썼던것처럼.

E는 T 타입을 만족한다 라는 의미를 갖는다.
예를 들어 아래와 같이 표현할 수 있다.
- 2 : int
- true : bool
- 2 * (3 + 4) : int
- “Hello” : string
- if (b) 2 else 3 : int
- x == 10 : bool
- y = 2 : int 또는 y=2 : unit
unit 는 well typed 임을 표현한다. C언어 같은 경우 RHS의 값을 결과값으로 간주해서 y = 2의 타입이 int라고 판단하는데, 그렇지 않는 언어의 경우 y = 2라는 statement의 결과값은 존재하지 않지만 type과 관련된 부분에서 이상이 없을 때 well typed라고 한다.
🌱 타입 Judgment
예를 들어 if (b) 2 else 3 : int라고 가정하고 싶다. 이처럼 가정하기 위해 사전에 알아야 할 정보는 아래와 같다.
- b : bool
- 2 : int
- 3 : int
2, 3이 integer라는 것은 쉽게 알 수 있지만, b가 boolean인지는 명시되어있지 않다. 이런 가정이나 상황을 확실히 표시하기 위해 아래와 같은 문법을 사용한다.
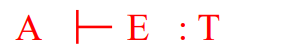
A 상황에서 E는 T 타입을 만족한다는 의미를 갖고 있다. 이때 A부분에는 symbol table이 온다고 생각해도 좋다.
예를 들어 아래와 같이 사용할 수 있다.
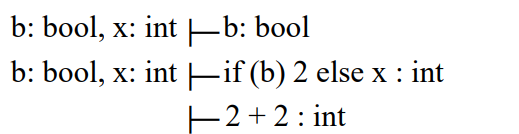
위 문법을 이용해서 if (b) 2 else 3 : int를 표현해보면 아래와 같다.
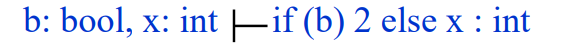
하지만 위와 같이 작성하기 이전에도, 다음과 같은 가정이 우선되어야한다.
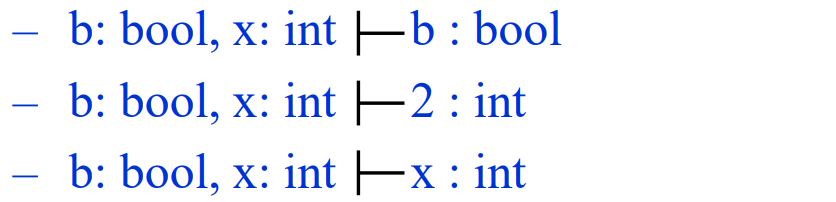
위와 같은 과정을 일반화할 수 있다. 이렇게 정리한 일반적인 추론(inference) 규칙은 다음과 같다.
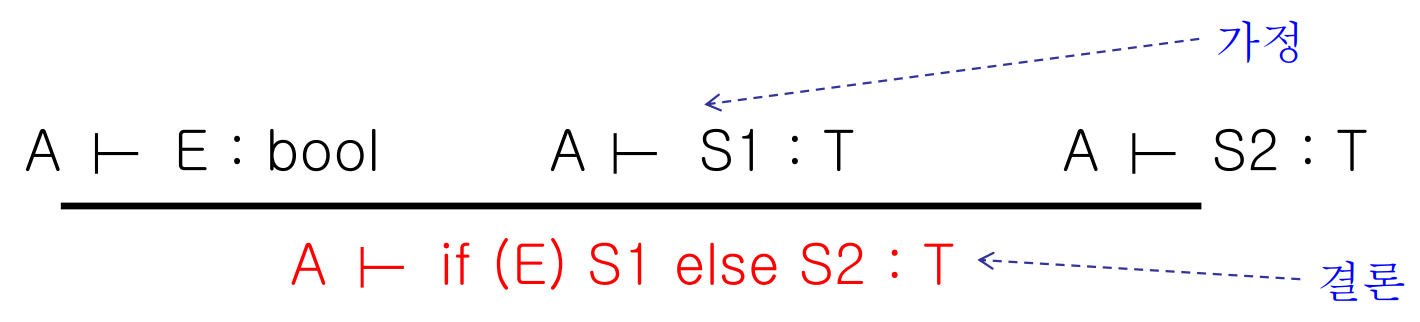
모든 E, S1, S2, A, T에 대해 가정이 성립하면 결론이 성립한다는 의미를 갖고 있다. 이 규칙을 기반으로 타입체킹을 진행한다.
🌱 Proof Tree(타입 유도 트리)
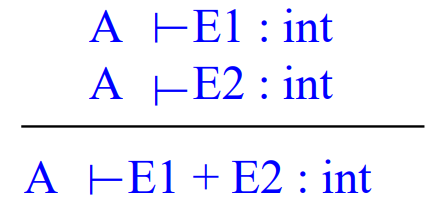
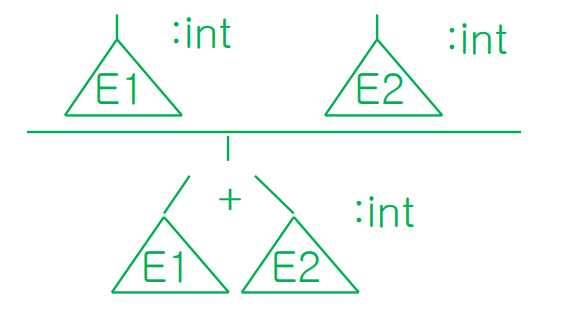
int와 int를 덧셈하면 결과값의 타입이 int가 된다. 이를 위에서 정의한 타입 judgment 규칙 형태로 도식화하면 왼쪽과 같다.
그런데 E1과 E2는 그 자체로 int타입의 값 하나가 아니라 또다른 식들이 될 수 있기 때문에 E1과 E2도 각각 본인의 타입 judgment 규칙으로 풀어야하고, 그렇게 모두 풀면 오른쪽 그림과 같은 다이어그램이 위로 쭉 퍼진 역트리 형태가 될 것이다.
즉 타입 judgment 규칙이 역트리모양으로 구성되고, 이를 proof tree라고 한다. 어떤 가정에 대해 만족하는 proof tree가 그려진다면 타입 오류가 없다는 것과 같다.
proof tree의 예시는 다음과 같은 경우가 있다. 이때 A1이란 b : bool, x : int를 편의상 짧게 표현한것이다.
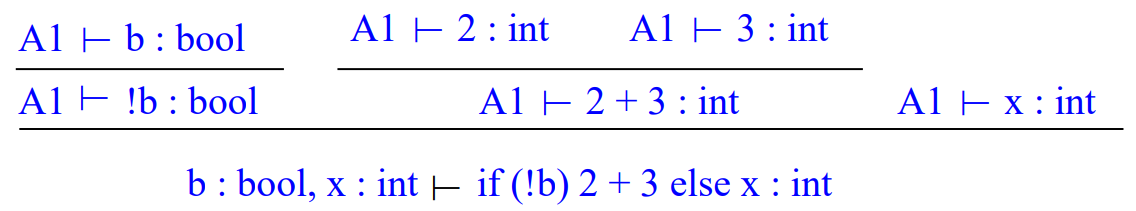
Assignment Statements를 proof tree로 나타내면 다음과 같다.
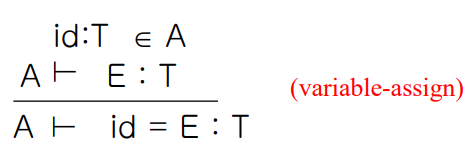

If Statements를 proof tree로 나타내면 다음과 같다.
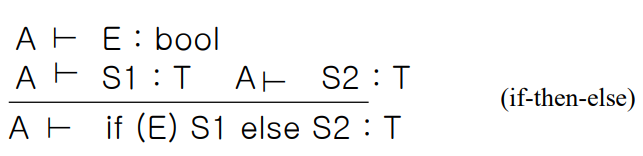

If Statement에서 else가 없는 경우에는 결과 타입을 확정해줄 수는 없지만 무엇이 되어도 괜찮기 때문에 unit이라고 표기한다.
📝 문제 풀어보기
f1 [ 3 ]
i = i1 [ i2]
while (i < 10) do S1
(i == 0 ? 4.0 : 1.0 )
다음 문장의 type 은?
단 i로 시작하는 식별자는 int 변수거나 int 타입을 원소로 하는 배열 이고, f로 시작하는 식별자는 float 변수거나 float 타입을 원소로 하는 배열이라고 가정한다. S1은 타입이 오류가 없는 문장이다.


왼쪽과 같은 언어에 대해 오른쪽과 같은 타입 규칙이 있을 때, 다음 문장의 타입을 트리로 유도하시오.
(1) if iszero 0 then 0 else pred 0 : int
(2) pred(succ(iszero(succ(pred(0))))) : int
while (E) S 을 위한 추론 규칙을 정의해보시오.



