목차
2023학년도 2학기 충남대학교 조은선 교수님의 컴파일러개론 수업 정리자료입니다.
이제부터는 물리적인 제약조건도 생각하자.

컴파일러 후반부는 빠른 코드로 바꾸는 최적화 부분과 실제 머신에서 도는 코드로 바꾸는 부분으로 나뉜다.
회색 부분이 실제 머신에서 도는 코드로 바꾸는 부분.
Machine-independent Optimization부분은 CPU나 컴퓨터구조와 관련없는 부분.
아래부분은 좀더 물리적 제약조건이 있고 머신 각각에 특화된 최적화를 하기 위해 노력하는 부분.
이번 시간에는 Instruction Selection과 Instruction Scheduling과 Register Allocation부분을 다뤄보자.
📁 Instruction Selection
명령어를 할당하는 것을 insturction selection이라고 부른다.
보통 트리 형태의 중간코드로부터 시작한다. gcc 같은 경우 세 단계의 중간코드로 이루어져 있고, 가장 하이레벨 언어에 가까운게 트리형태 AST에서 바로 변형된 트리형태. 가운데가 3-addr 코드. 제일 기계어랑 가까운게 RTL이었는데, 이게 트리모양의 구조를 갖고있음.
RTL로 바로 설명하면 좋겠지만 좀 복잡해서, 그보다 좀더 HIR중 하나인 트리 기반의 IR을 다룰것임.

CONST나 BINOP 등의 표현들을 보면 low level 형태의 노드들이 있음을 알 수 있음.
이 IR은 다음과 같은 규칙을 갖고 있다.
- MEM(e) : 주소 e 로 시작하는 메모리 한 word 의 내용. MOVE의 왼 쪽에 사용되면 store, 다른 곳에 사용되면 fetch의 의미.
- TEMP(t) : 레지스터 t
- SEQ (s1, s2) : 문장 s1 수행후 s2 수행. 마지막이 statement이기 때문에 결과값이 따로 없음을 나타냄.
- ESEQ(s,e) : 문장 s는 결과는 없고, side effect만 가지므로 ESEQ 전체의 결과를 내기 위해서는 e가 추가 수행됨. 마지막이 expression이기 때문에 결과값이 있음을 나타냄.
- BINOP(o, e1, e2) : o는 PLUS, MINUS와 같은 binary operator. 결 과는 피연산자 e1, e2를 가지고 이 o를 수행한 것. 결과는 메모리에 저장 후 주소 리턴
- const(i) : 정수 상수 i

이렇게 동치 관계를 갖는 트리를 구해서 가장 비용이 낮은 것을 선택하는 과정이 최적화이다.
일반적으로 명령어의 실행 순서와 결과값이 같으면 동치관계라고 판단한다.

왼쪽 트리의 경우 e1, s, e2 순서로 실행하고, 마지막에 결과적으로 BINOP를 수행한다.
오른쪽 트리를 보면 e1을 먼저 실행하여 Temp t인 레지스터에 MOVE한다. 이후 s를 수행하고, ESEQ의 오른쪽이 BINOP이므로 이부분이 결과값으로 나오는데, e2를 실행한 후 e1를 계산한 값을 넣었던 t와 BINOP를 수행한 결과가 최종 결과값이다.
보통 오른쪽이 더 선호된다. 예를들어 e1을 계산해서 t에 넣어두고 다른곳에서 이 결과값을 사용하는 경우나, e1결과값을 바로 사용한다고 하더라도 레지스터에 담아둠으로써 연산을 줄이는 효과를 얻기 때문이다.

s가 e1다음에 실행되건 e1 앞에 실행되건 결과가 달라지지 않는 경우에만 왼쪽의 두 트리가 동치이다.
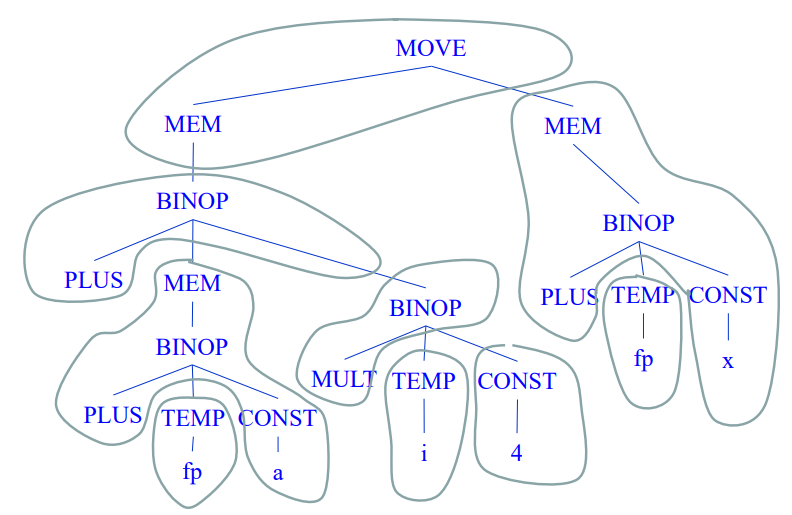
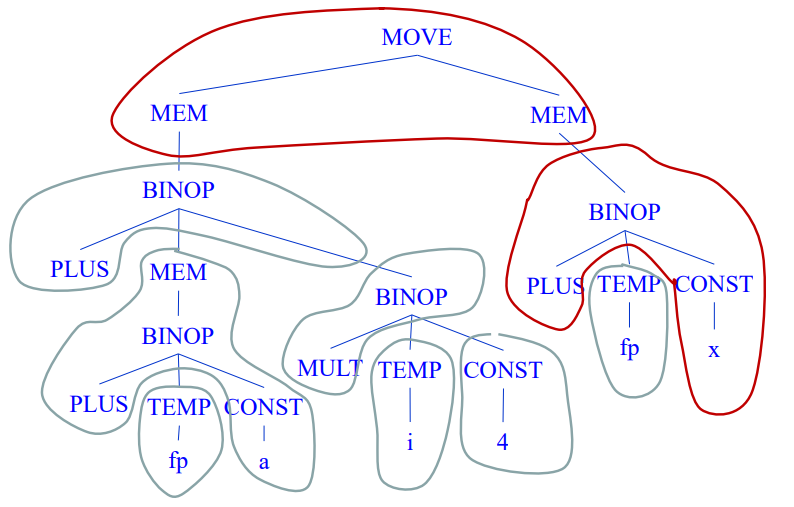
위에서 묶은 Group은 instruction의 단위를 뜻한다.
왼쪽의 MEM과 MOVE를 하나의 인스트럭션으로 볼 것이냐, MEM과 MOVE, MEM을 하나의 인스트럭션으로 볼 것이냐에 다라 두가지 옵션이 있다.
이를 Machine Code 형태로 보면, 다음과 같은 사례가 된다.

머신에서 Memory to memory store를 지원하면 두번째 옵션을 사용하게 되고, 대부분의 머신은 이를 지원하지 않기 때문에 첫번째 옵션을 사용한다.
즉 Instruction Selection이라는 것은 머신이 제공하는 instruction set에 맞춰서 더 효율적이고 빠른 instruction을 선택하는 것이다.
📁 Register Allocation
Low Level IR을 복습해보자.
3-addr 등에서 중간에 임시변수 레지스터가 무한히 존재한다고 가정했었음. 이게 integer나 scalar 변수라면 메모리가 아니라 레지스터에 할당될 것. 이게 개수가 몇갠지를 잘 생각 안했었음. 가상 레지스터가 무한히 있다고 생각했었지만, 이게 진짜 무한하지 않음. 이걸 진짜 유한한 레지스터에 넣는 작업이 Register Allocation.
Register allocaiton이 추구하는 것은 가상 레지스터를 최대한 물리적 레지스터에 넣고, 남는 것들을 메모리에 넣는 것. 이걸 spilling이라고 함.
🌱 Interference
interference란 서로 다른 두 변수가 공통 live range를 가지는 것.
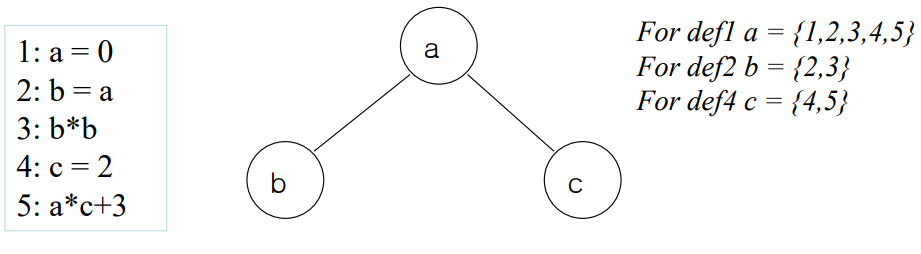
예를 들어 1번에 0으로 초기화된 a가 2번과 5번에 사용되고 있다. 여기서 a의 live range는 정의된 이후 사용되는곳까지, def-use 관계 전체를 이야기한다.
즉 def1 a = {1,2,3,4,5}란 1,2,3,4,5란 def1 a가 살아있어야한다는 뜻.
def란 보통은 assignment를 의미.
이때 저 중괄호가 live range이고, live range는 liveness 분석과 reaching definition 분석 두가지를 응용하여 만들어진다.
b와 c는 live range가 서로 겹치지 않는다. 그래서 b와 c는 하나의 같은 피지컬 레지스터를 할당해도 문제가 없다.
서로 live range가 겹치는 definition들을 찾기 위해 위 그림처럼 변수를 노드로 작성하고 live range가 겹치는 변수끼리 줄을 잇는다.
🌱 Graph Coloring
레지스터를 allocation할 때 Graph coloring이라는 알고리즘을 사용한다.
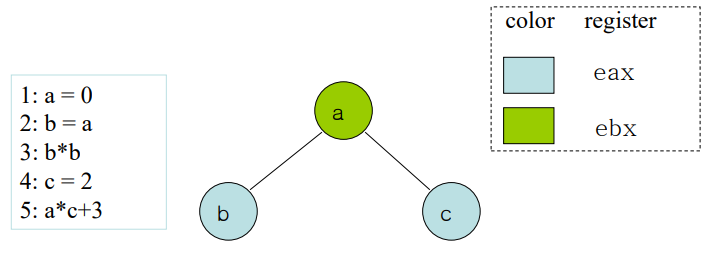
서로 떨어져있으면 같은 색을 칠해도 되지만, edge를 공유하면 다른 색을 칠해야하는 알고리즘.
색깔이 곧 레지스터라고 가정.
K-Graph Coloring Algorithm은 굉장히 오래된 문제임.
Step 1. simplify
k보다 작은 edge를 가진 node를 찾아서 edge와 함께 잘라낸다. 그리고 이 node를 stack에 저장한다.
Step 2. color
나머지 simplified subgraph로 쉽게 k-graph coloring을 할 수 있으면 stack에 있는 node를 pop해서 연결된 node에 없는 색깔 칠하기를 반복한다.
Step 3. Spill
Step 1, 2로 해결되지 않는 경우 변수 몇개를 골라서 메모리에 저장한다.
예를 들어보자.
Step 1.
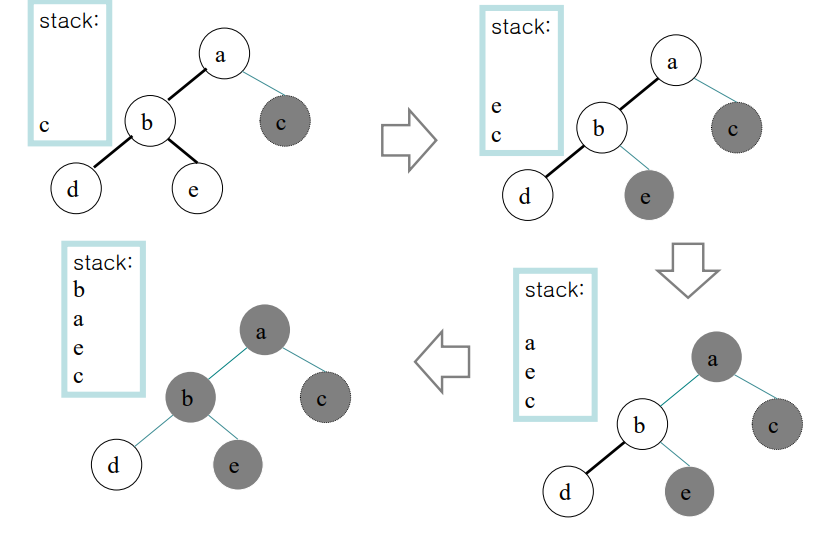
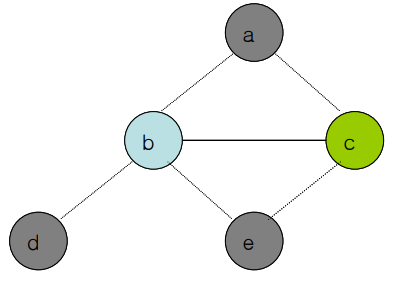
연결된 edge가 k=2보다 작은 한개인 노드들을 랜덤으로 선택하여 제거한다. 가장 먼저 d, e, c 중 c를 제거한다.
다음으로 d, e, a중 e가 선택된다. 이전 단계에서 c를 edge와 함께 제거했으므로 a의 edge는 한개만 남은것이다.
다음으로 d, a중 a가 선택된다.
Step 2.
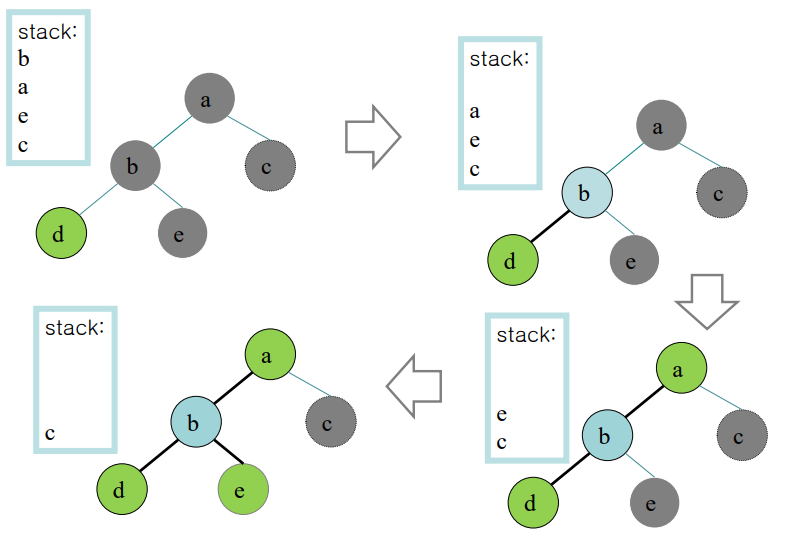
남아있는 d에 먼저 아무 색깔을 칠해준다. 이후 stack top을 꺼내서 연결된 노드의 색과는 다른 색으로 칠해준다.
위 사례의 경우 Step 3가 발생하지 않는다.
하지만 만약 모든 노드가 같은 수의 edge를 갖고있으면 어떻게 할까? 아래 사례논 d가 stack에 들어간 이후 모든 노드가 2개의 edge를 가지고 있는 경우이다.
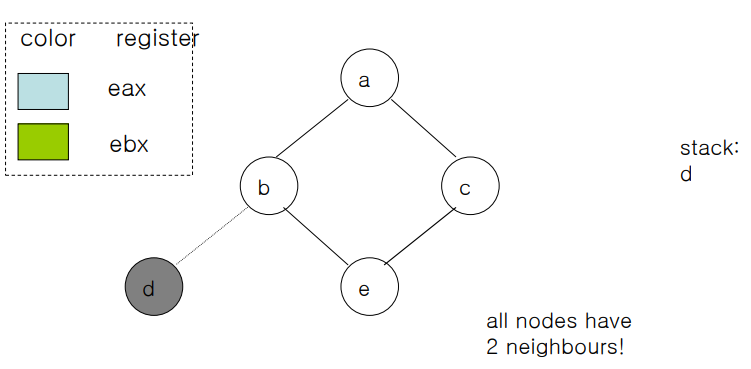
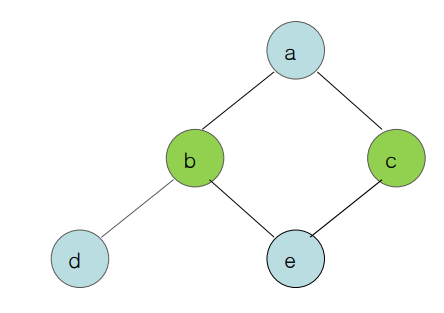
하지만 오른쪽과 같이 솔루션은 존재한다. 즉 이 알고리즘은 솔루션이 있다고 해도 모든 문제를 풀어주지 못한다. 하지만 대부분 풀 수 있어서 잘 이용되고 있다.
위 경우, 2개의 색깔로 절대 coloring할 수 없는 그래프이다. 이는 k-color algorithm으로 해결할 수 없으며, 실제 솔루션도 존재하지 않는다. 이런 경우 Spilling을 진행한다.
🌱 Spilling
Spilling은 어떻게 이루어질까. 코드를 다시 고쳐 써야한다.
예를 들어 t2를 메모리에 넣기로 결정한 상태에서 add t1, t2라는 코드가 존재한다고 가정하자.
t2와 연결된 메모리, 즉 t2를 메모리의 어느 영역에 정의하고자 한다면 스택의 [ebp-24]에 t2가 임시변수 영역에 매핑될것.
그다음 새 레지스터인 t35를 하나 도입한다.
add t1, t35 이렇게 덧셈을 하고, t1과 t35는 둘다 피지컬 레지스터. 그런데 이때 t35는 t2를 매핑했던 [ebp-24]에서 가져오는거. 메모리에 t2값이 있고 이걸 t35로 가져와서 계산하는 과정.
그런데 레지스터가 부족해서 t2를 메모리에 넣었는데 t35를 어떻게 쓸수 있을까? 사실 t35라는 레지스터는 특수한 레지스터라서 live range가 아주 짧다. 위와 같은 경우 mov, add 이후 끝난다. 그래서 interference 가능성이 거의 없다.
예를 들어 기계어 코드에서 특정 레지스터가 엄청 많이 쓰이는 경우가 보인다면 그 레지스터는 t35와 같은 성격의 spill 전용 레지스터일 확률이 높다.
📁 Instruction Scheduling
Instruction scheduling의 역할은 instruction의 순서를 바꿔서 수행 속도를 높이는 것이 목적이다. 하지만 각각 실행속도가 변하는 것은 아니라서 도움이 안된다고 생각할 수도 있지만, stall 수가 줄어든다는 면에서 실행속도가 빨라진다.
앞서서 수행되어야하는 명령을 기다리느라고 CPU가 쉬는 경우를 stall이라고 한다.
insturcion마다 수행할때마다 드는 clock cycle 수가 다르다. 그 수가 아래와 같다고 가정해보자.
LOAD, STORE : 3 cycles
LOAD (not in cache) : 100s
ADD, SHIFT: 1
MULT : 2
DIV : 40
BRANCH : 0-8
기본적으로 요즘 컴퓨터들은 한 사이클마다 여러 opration을 실행시킬 수 있따.
그래서 실행시간 자체는 오퍼레이션 실행 순서에 좌우되고, 결과가 나오기 전까지 결과를 이용하는 오퍼레이션을 실행시킬 수 없더라도 다른일을 하는 오퍼레이션을 실행시킬 수 있다.
예를 들어 w가 w*2*x*y*z의 결과를 취한다고 가정하자.
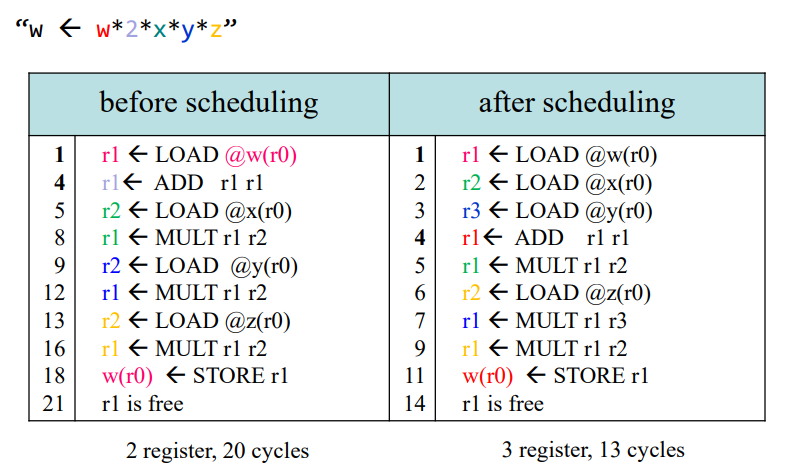
MULT 같은 경우, 8번 사이클에서 시작했지만 이 결과를 기다릴 필요 없이 9번 사이클의 LOAD가 바로 시작해도 된다.
이런 최적화 가능성을 고려해서 오른쪽과 같이 scheduling하면 13사이클로 줄지만, 사용하는 레지스터는 3개로 증가한다.
일반적으로 오른쪽이 선호된다.
instuction scheduling에서 wasting time을 줄이면서도 동일한 코드가 나ㅗ아야하고, 레지스터 사용을 너무 많이 하면 안된다는 challenge가 있다.
이를 위해서 다음 조건들을 만족할 수 있다.
- instruction 전에 모든 operand가 준비되어야한다.
- 여러 operation이 동시에 준비되어 있어야 한다.
- operation을 옮길때 register lifetime이 길어지는 것을 고려해야한다.
- use-def간 거리가 짧을수록 좋다.
- operand가 동시에 여러 dependency를 가질 수 있는 것을 고려해야한다.
- cashe miss등의 상황때문에 Latencies, 즉 명령어가 실행할때 걸리는 사이클 수는 이론처럼 항상 일정하지 않는다. 등등.
🌱 Static Scheduling
위와 같이 instruction scheduling이 복잡한 문제이긴 하지만, 이를 조금 해결할 수 있는 방법이 있다.
Local basic scheduling, Loop scheduling, global scheduling으로 3단계의 스케줄링이 있고, 이 3단계중 가장 간단한 단계인 basic scheduling을 살펴보자.
우리가 지금 하는 스케줄링은 컴파일 때 진행되는 static scheduling이다.
basic scheduling이란 블럭 안의 스케줄링으로, 코드 안에 점프 없이 작은 조각이 있다고 하면 그 안에서 로컬한 스케줄링.
Local basic scheduling은 List scheduling을 사용한다. List scheduling이란 오랫동안 사용되어온 greedy, heuristic, local 기술이다.
절차는 다음과 같다.
preceduence graph를 만든다.
그래프의 각 노드에 priority function을 적용한다.
"ready-operation queue"를 두고, 매 cycle마다 ready operation queue에서
📝 문제 풀어보기
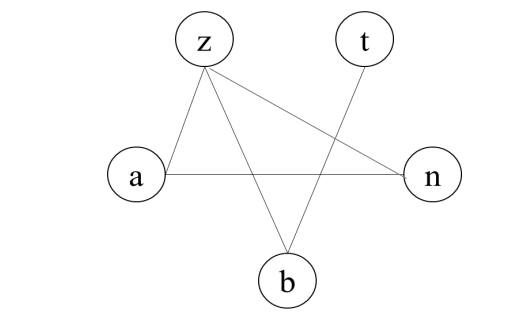
CPU에 r1, r2, r3 의 3개의 register가 이용 가능한 경우 오른쪽과 같은 interference 그래프에 대해 register allocation을 해보시오.



