목차
📁Binary Images
Binary Image란, 이미지 전체를 0과 1로 표현한 이미지를 말한다.
보통 알파벳 B로 이미지를 표현한다. B[r, c]는 binary image B의 row r, column c번째 픽셀을 말한다.
B[r, c] = 1이면 [r, c]는 foreground pixel, black pixel이라고 말하고
B[r, c] = 0이면 [r, c]는 background pixel, white pixel이라고 말한다

binary image의 값은 intensity와 반대이다.
보통 HEX값과 같이 색을 값으로 나타낼때는 0에 가까워질수록 검정색, 1에 가까워질수록 하얀색이지만
binary image에서는 단순히 칠해져있으면 1, 아니면 0으로 가정한다.
📁 Neighborhoods
어느 픽셀에 대해 neighborhood(이웃) 픽셀을 정의하는 방법은 두 가지가 있다.
4-neighborhood N4

{A, B, C, D}가 X의 4-neighborhood이다.
즉 위아래 양옆 네 방향의 픽셀을 이웃으로 정의한다.
8-neighborhood N8

{A, B, C, D, E, F, G, H}가 X의 8-neighborhood이다.
즉 4-neighborhood에서 대각선방향의 네 픽셀도 포함하여 여덟 방향의 픽셀을 이웃으로 정의한다.
📁 Connectedness
위에서 정의한 두 방법의 neighborhood를 이용하여, connected component를 찾는 방법도 두가지로 분류된다.
4-neighborhood N4

A와 H는 이웃으로 연결이 가능하지만, K와는 연결이 불가능하다.
그림에서는 {A, B, C, D, E, F, G, H} / {I, J, K, L, M}와 같이 연결 가능한 픽셀들이 두 묶음으로 나뉜다.
위 두 집합을 connected component라고 부른다.
8-neighborhood N8
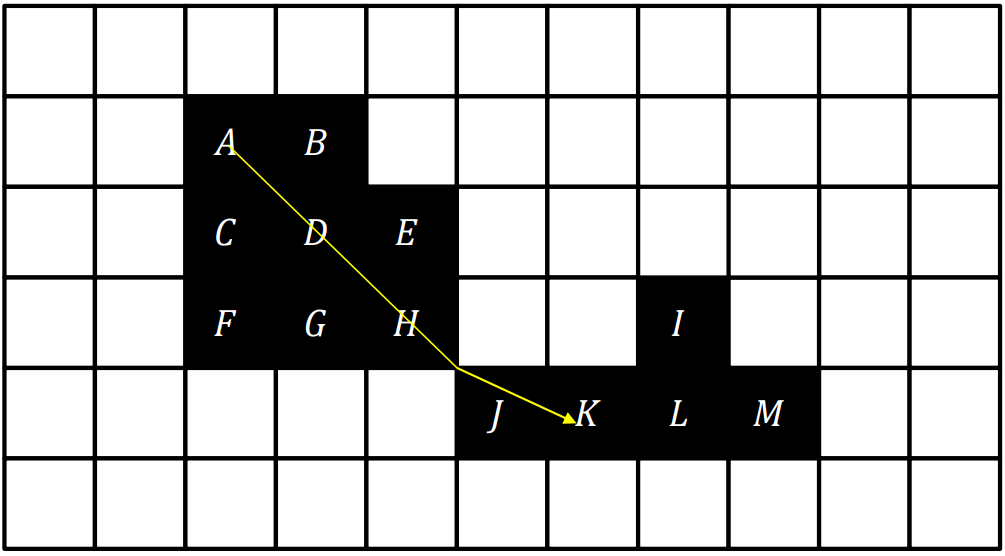
A와 모든 알파벳들이 이웃으로 연결 가능하다.
위 그림에서는 {A, B, C, D, E, F, G, H, I, J, K, L, M}와 같이 연결 가능한 픽셀들이 하나의 집합이 된다.
8-neighborhood 방법에서 "{A, B, C, D, E, F, G, H}는 connected component이다" 라는 말은 틀린 말이다.
📁 Connected Components Labeling
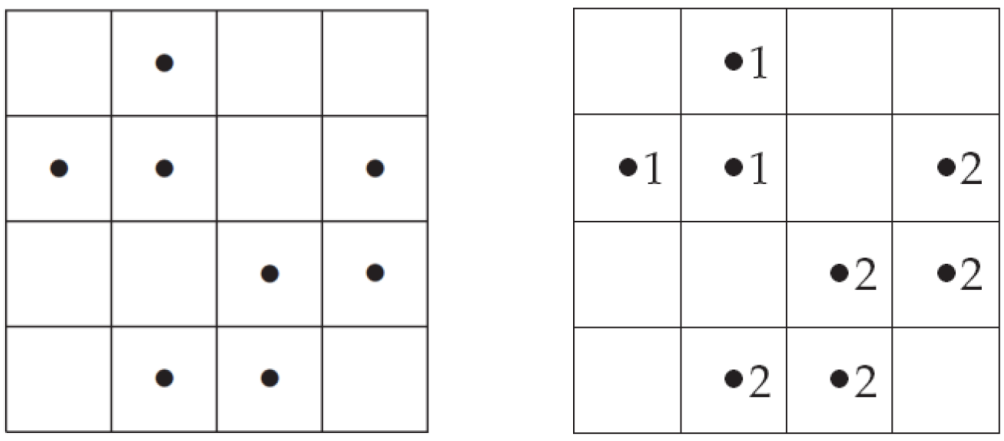
connected component에 각각 라벨을 붙이고자 한다.
각 connected component에 다른 이름을 붙여 개체를 구분함으로써 이를 이용한 연산이 더 수월해진다.
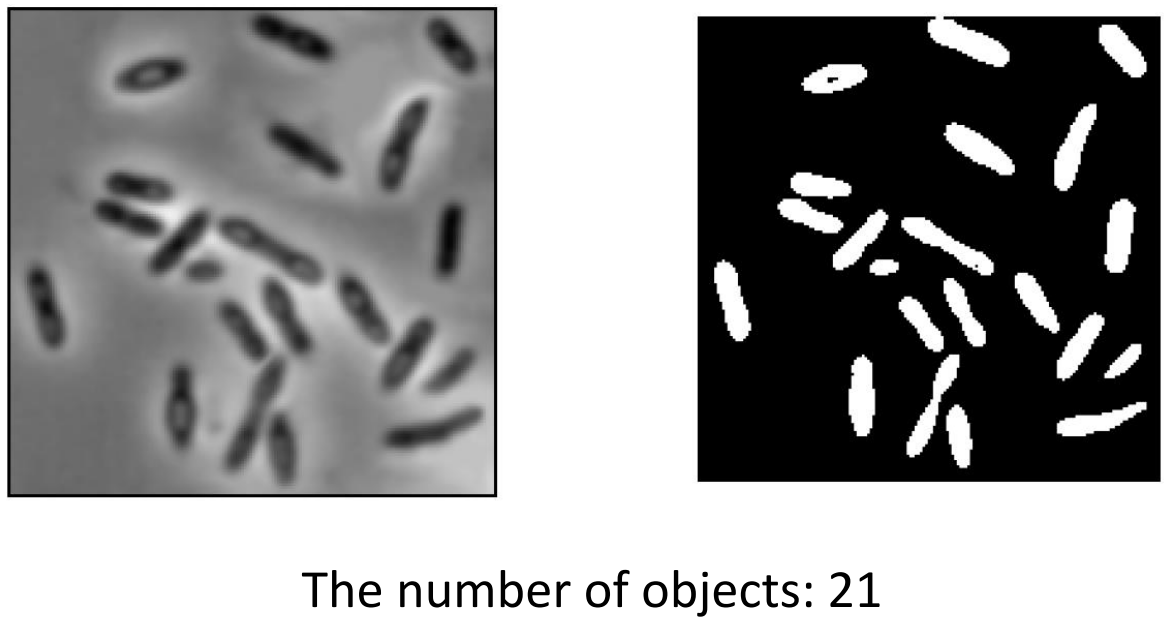
예를 들어, 위 이미지에 검은색 타원의 개수를 구할 때, 각 connected component를 1번부터 라벨링하면 마지막 라벨의 숫자가 곧 개체의 개수가 된다.
이외에도 이미지 내에서 개체들을 다루고 구분하기 위해서는 각각 다른 이름을 붙일 필요가 있기 때문에 Labeling 작업이 필요하다.
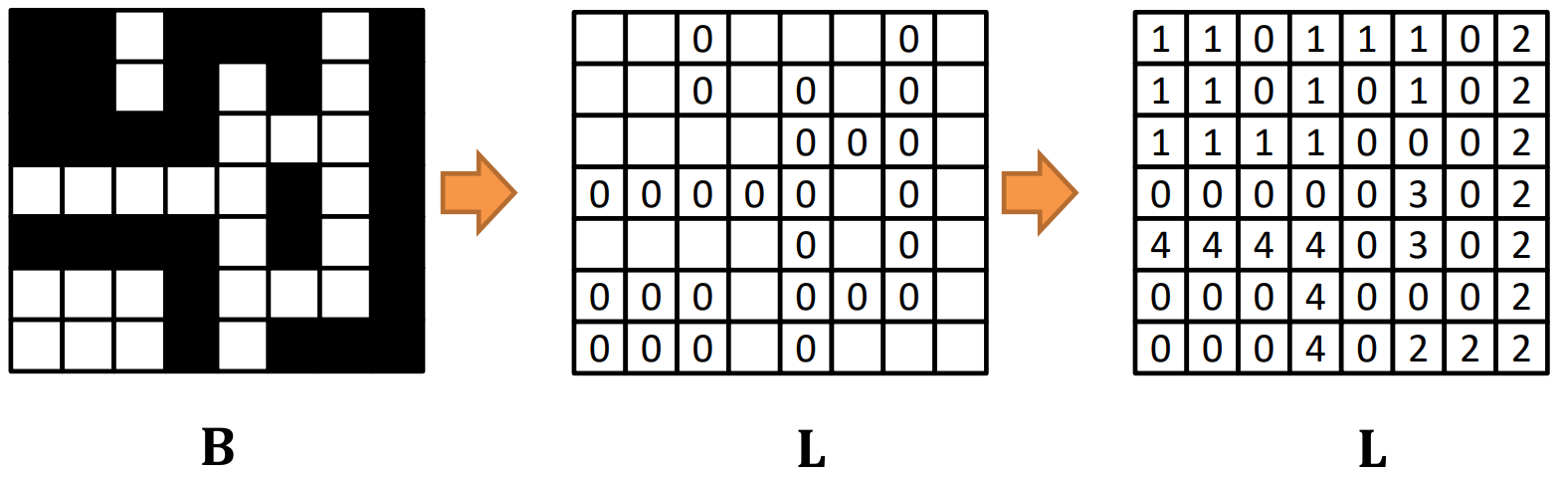
labeling을 위해서는 먼저 binary image의 background pixel 값을 모두 0으로 할당하고, 나머지 빈 부분을 적절한 알고리즘을 사용하여 채우는 방식을 이용한다.
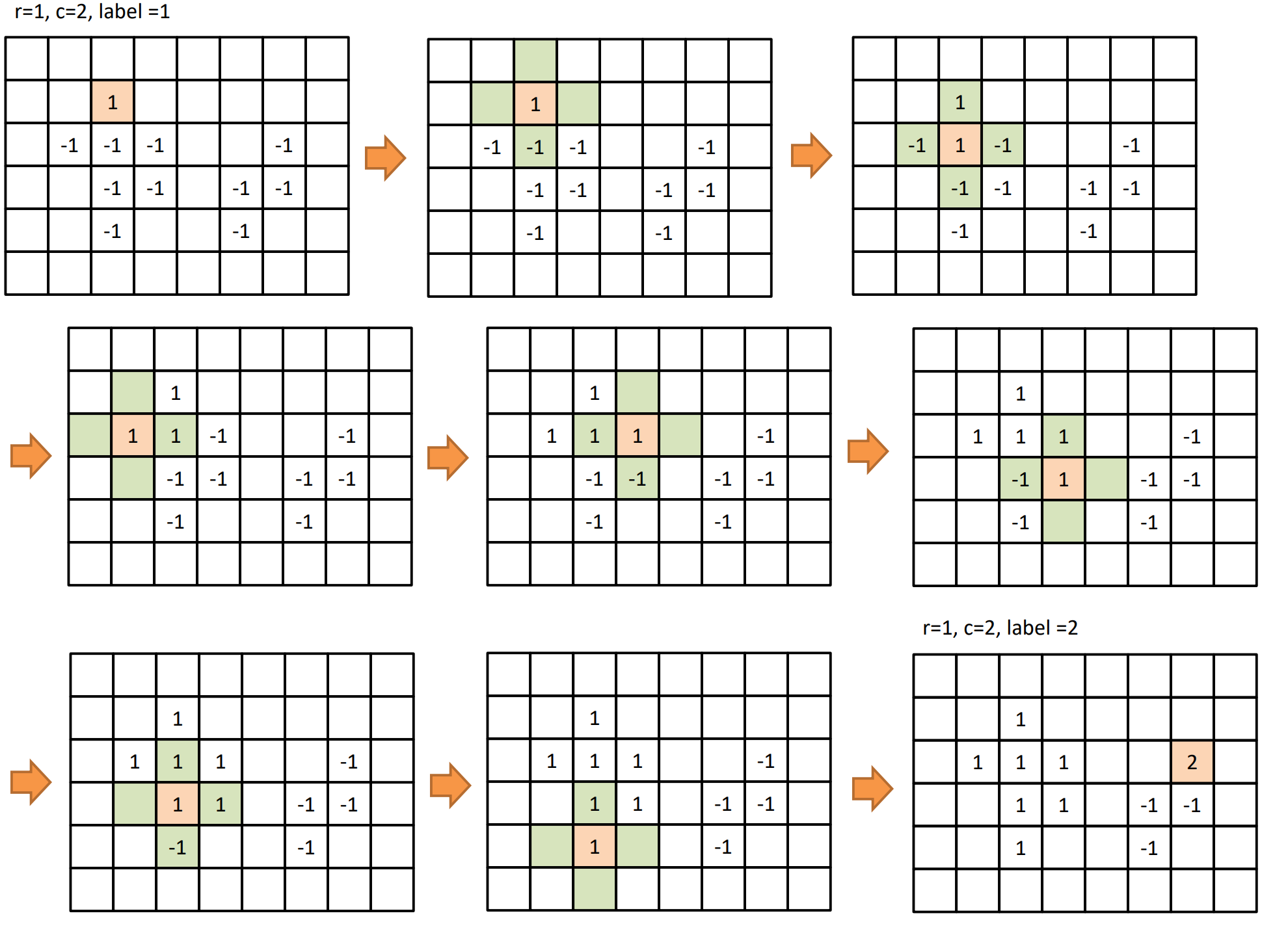
이때 Recursive labeling 알고리즘을 사용할 수 있다.
recursive labeling방법을 이용하면 이미지의 모든 픽셀에 random access가 가능하다.
이때 random access란 요소에 비순차적으로 접근하는 것을 말한다.
한가지 특정 순서로만 모든 요소를 방문할 수 있는 sequential access와 반대되는 개념이다.
random access는 요소의 주소를 알고 있다면 요소의 개수와 무관하게 보다 쉽고 효율적으로 접근이 가능하다는 장점이 있다.
만약 개체를 찾기 위해 binary image에서 0이 아닌 값을 하나 찾았다고 하자.
이후 neighborhood를 찾기 위해서 첫번째 픽셀부터 순차적으로 접근할 필요 없이, 현재 접근한 픽셀 위치를 기준으로 값이 0이 아닌 이웃 픽셀을 찾으면 되므로 recursive labeling 방법을 사용한다.
📁 Binary Image Morphology
Morphology는 형태학이라는 뜻으로,
영상처리 분야에서는 이미지를 형태학적으로 다루는 기법을 말한다.
즉 이미지 내의 여러 형태, image component들을 추출하고 이를 연산하는 것을 말한다.
위에서 설명한것과 같이 개체를 connected component, 픽셀의 집합으로 표현하면, 이를 이용해 set operation이 가능하다.
Morphology에는 다음과 같은 기본적인 operation들이 있다.
- Translation
- Dilatioin
- Erosion
- Closing
- Opening
📁 Translation(이동)
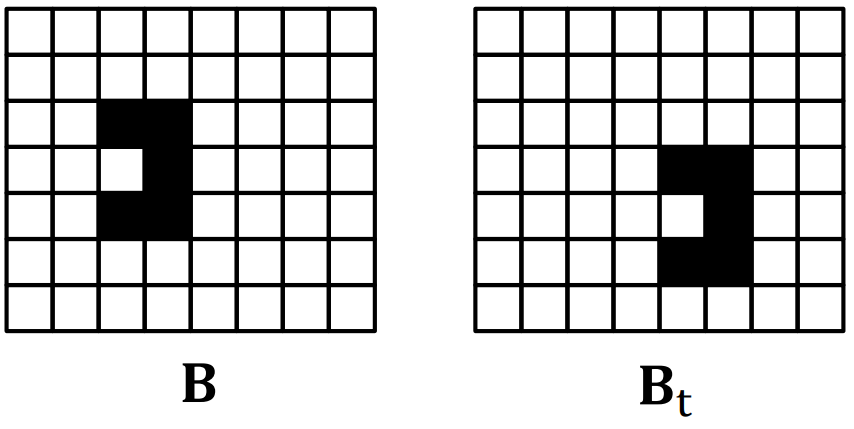
Translation은 개체를 다른 위치로 이동시키는 것이다.
position vector t = (u, v)를 이용한 B의 translation Bt 는 다음과 같이 정의된다.
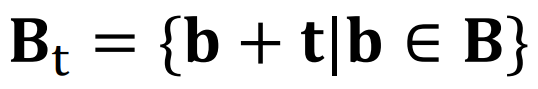
b는 input image인 B의 픽셀 coordinate들이고, b에 t를 더한 새 coodinate가 Bt를 이룬다.
📁 Dilation(팽창)
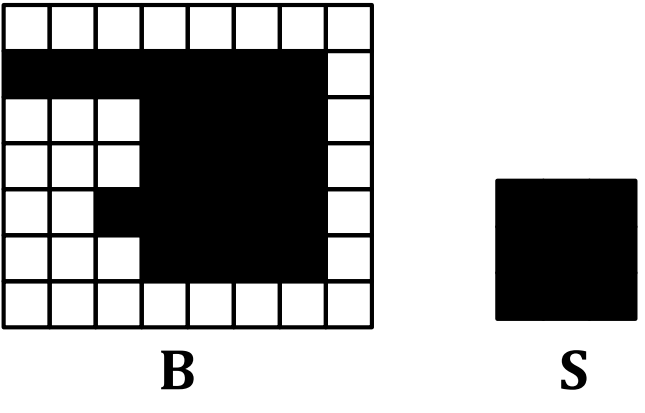
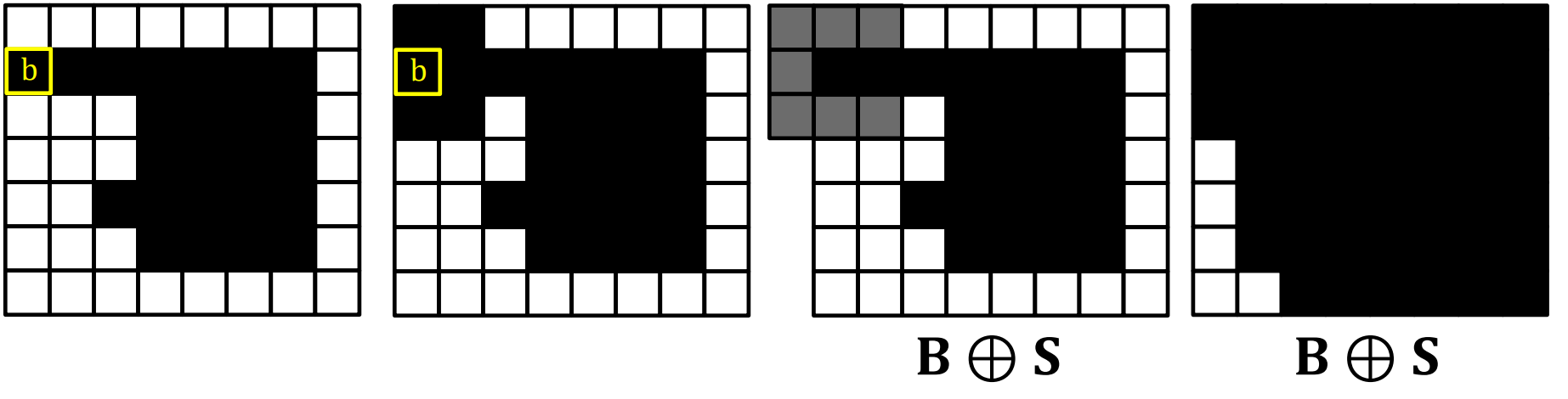
Dilation은 팽창이라는 뜻으로 black pixel의 영역을 넓히는 연산이다.
input binary image의 black pixel 위에 structing element의 중간 픽셀을 맞추어 놓아보고, 그 영역을 모두 black pixel로 바꾼다.
이 과정을 input image의 모든 black pixel에 대해 반복하면 결과가 나온다.
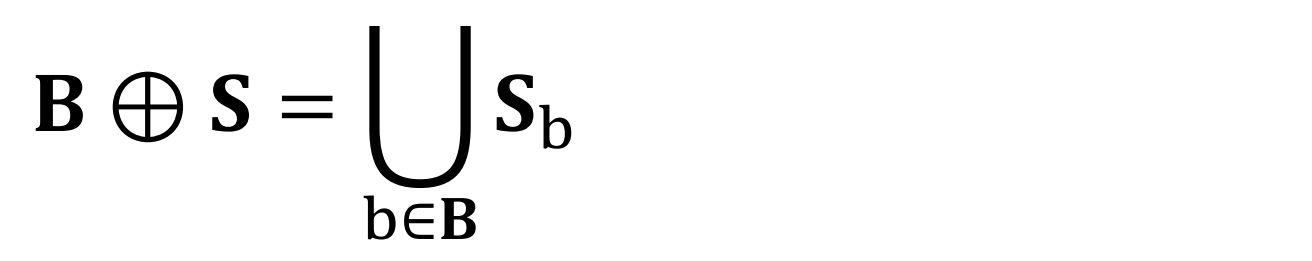
B는 input binary image,
S는 structing element,
Sb은 현재 픽셀인 b를 기준으로 S를 적용시킨 현재 픽셀의 팽창 영역을 말한다.
이를 모두 합집합 연산하면 output binary image가 나온다.

dilation을 이미지에 적용하면 위처럼 이미지가 뚱뚱해진다.
📁 Erosion(침식)
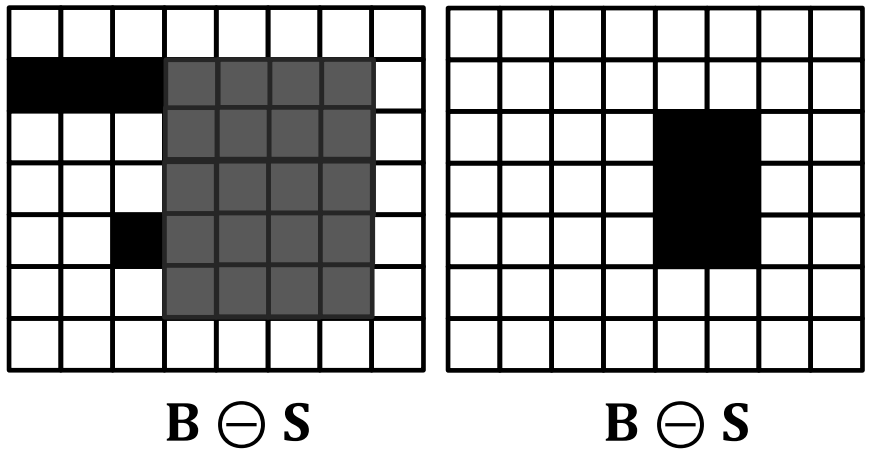
Erosion은 침식이라는 뜻으로, input binary image의 모든 black pixel들에 structing element를 적용하여 black pixel의 영역을 좁히는 연산이다.
input binary image의 black pixel 위에 structing element의 중간 픽셀을 맞추어 놓아보고, 그 영역의 모든 픽셀이 원본 이미지의 black pixel이 있던 영역이라면 해당 black pixel을 남긴다.
이 과정을 input image의 모든 black pixel에 대해 반복하면 결과가 나온다.
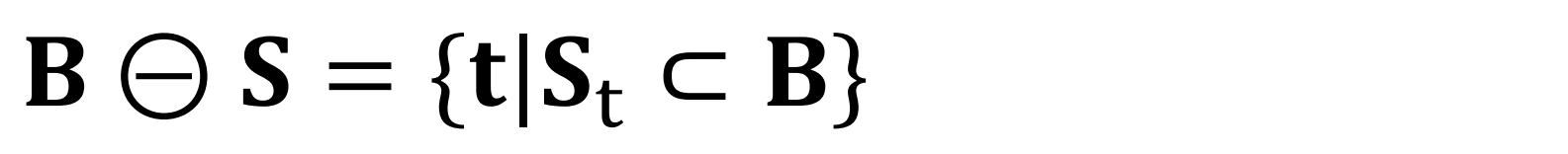
B는 input binary image,
S는 structing element,
t는 erosion 결과로 도출되는 black pixel들의 집합,
St은 t 픽셀 위에 S를 적용한 영역을 말한다.
t 픽셀 위에 S를 적용시켰을때, 이 영역이 B 안에 완전히 포함된다면 이때 t 픽셀들의 집합이 결과라는 의미이다.

erosion을 이미지에 적용시키면 위처럼 몇몇의 고립된 픽셀들을 제거할 수 있다.
📁 Opening
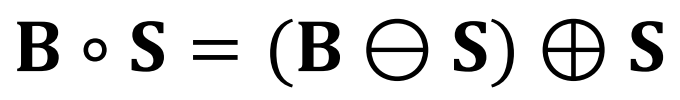
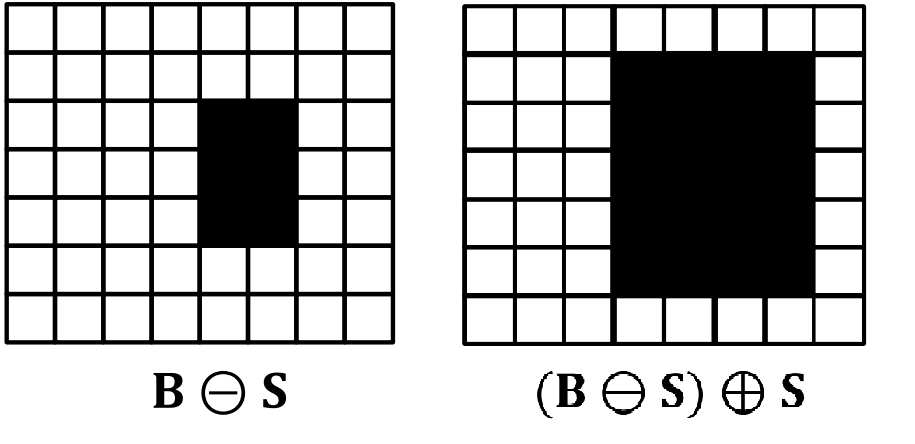
Opening은 input binary image B와 structing element S를 erosion 후 dilation하는 것이다.
input image보다 개체들이 더 작아지고, 작거나 얇은 부분들이 사라진다.
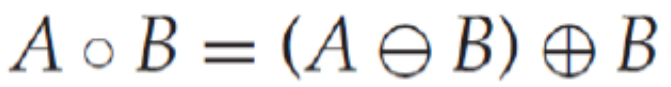
Opening은 이와 같이 하얀색 동그라미로 표현한다.

Opening의 결과는 무조건 input image에 포함된다.
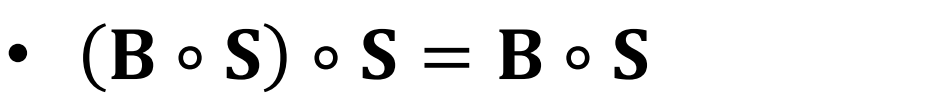
Opening의 결과에 몇번을 다시 Opening 해도 결과는 같다.
즉, 같은 input image와 structing element에 대해 Opening 연산의 결과는 유일하다.
이처럼 연산을 여러번 해도 결과가 같은 성질을 Idempotence(멱등성) 성질이라고 말한다.

input image B를 완전히 포함시키는 input image C가 있다면, 같은 structing element에 대해 두 이미지의 opening 결과는 같다.
Erosion vs. Opening
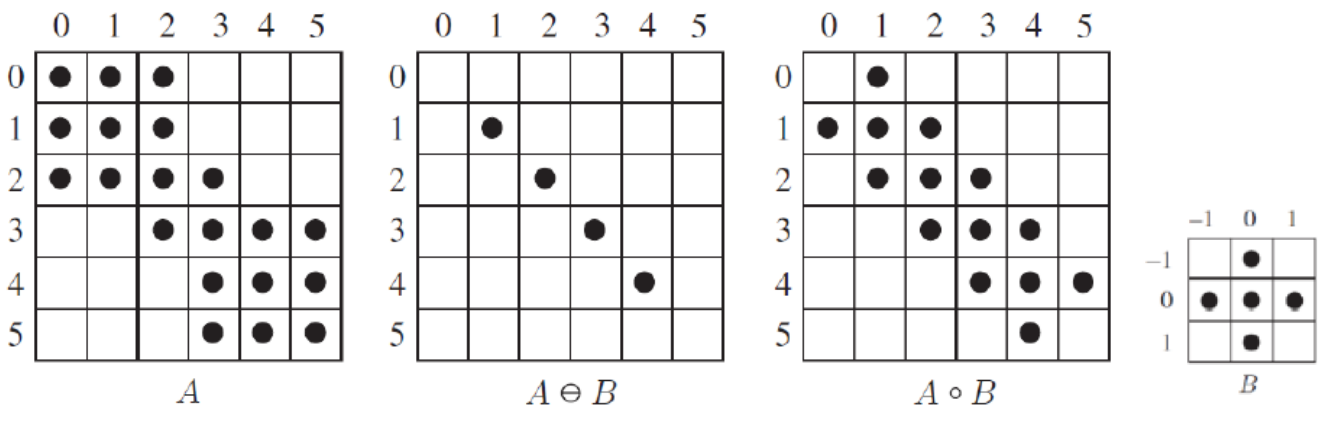
Erosion 결과를 두껍게 만드는 것이 Opening이다.

Erosion : 픽셀 w에 structing element B를 적용한 영역이 A에 포함될 때 모든 픽셀 w들의 집합
Opening : 픽셀 w에 structing element B를 적용한 영역이 A에 포함될 때 B를 적용한 영역의 집합
📁 Closing
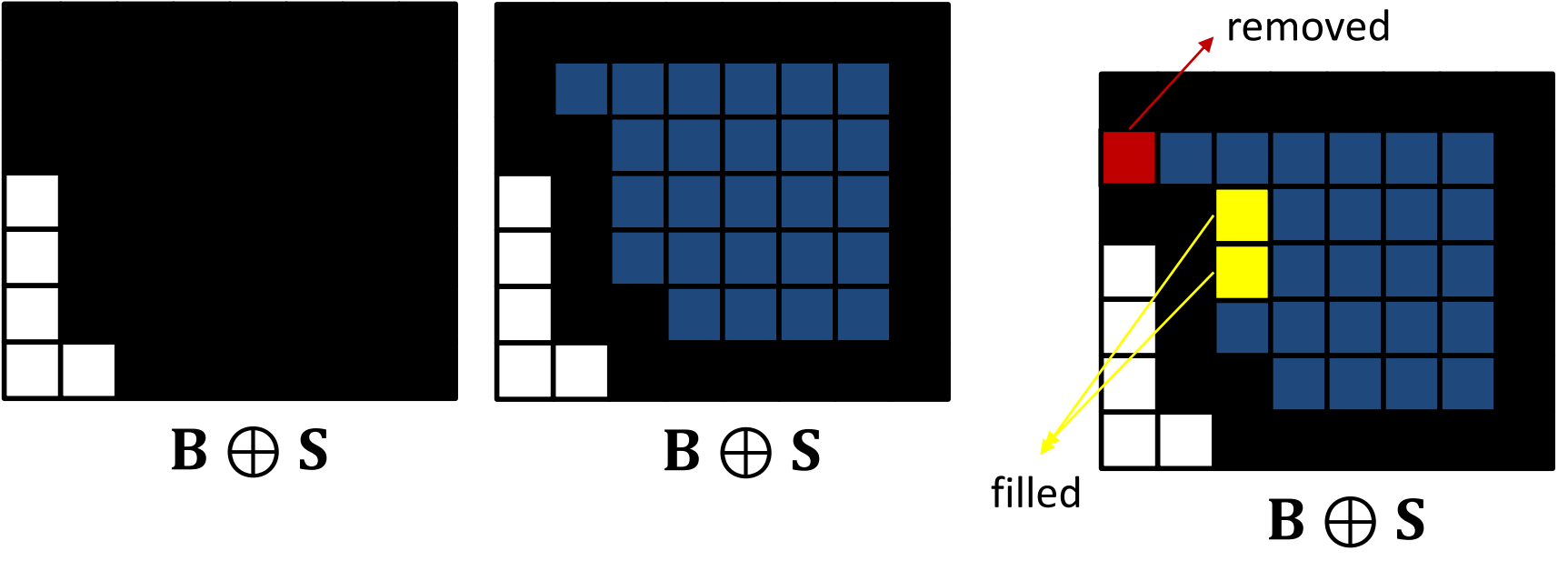
Closing은 input binary image B와 structing element S를 dilation 후 erosion 하는 것이다.
input image보다 개체들이 더 커지고, 모서리부분의 픽셀은 사라지고 얇은 빈부분은 채워진다.

Closing은 이와 같이 검은색 동그라미로 표현한다.

Closing의 결과는 무조건 input image를 포함한다.
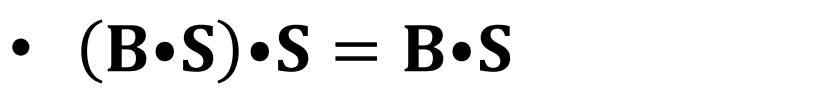
Closing 의 결과에 몇번을 다시 Closing 해도 결과는 같다.
Opening과 같은 Idempotence(멱등성)성질을 지닌다.

input image B를 완전히 포함시키는 input image C가 있다면, 같은 structing element에 대해 두 이미지의 Closing 결과는 같다.
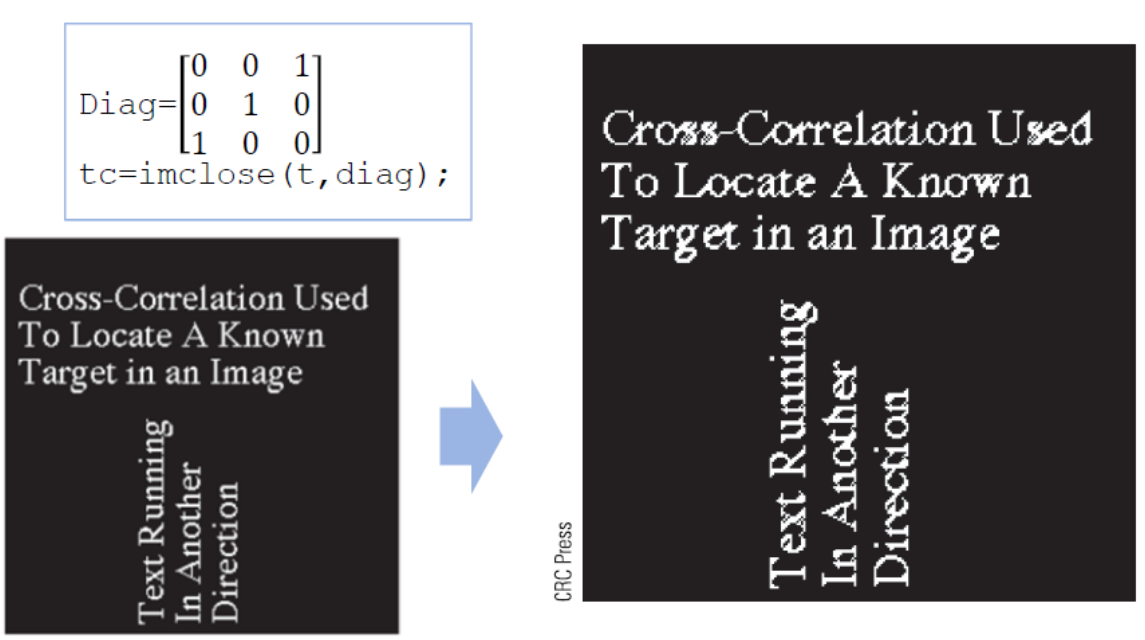
Dilation vs. Closing
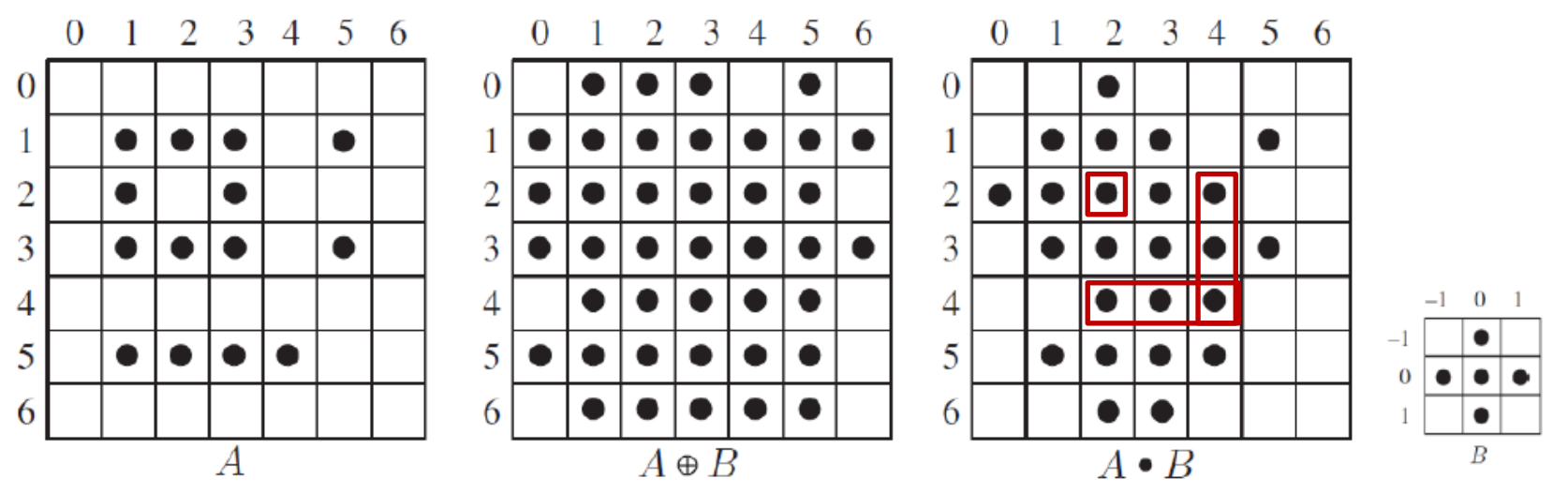
Dilation 결과를 얇게 만드는 것이 Closing이다.
Dilation : 픽셀 w에 structing element B를 적용한 영역의 집합
Closing : 픽셀 t에 structing element B를 적용한 영역이 Dilation 결과에 포함될 때 모든 픽셀 t들의 집합
🔎 Opening vs. Closing
Opening과 Closing 모두
이미지가 smoothing, 즉 부드러워지고
작은 오브젝트들이 삭제되는 공통점이 있지만
Opening은 이미지를 줄였다가 키우기때문에 black pixel 사이에 좁은 틈들을 연결해주지 않지만,
Closing은 이미지를 키웠다가 줄이기 때문에 키우는 과정에서 black pixel 사이의 좁은 틈이 연결될 가능성이 높다.
📁 Morphology 연산의 활용방법
Boundary Detection
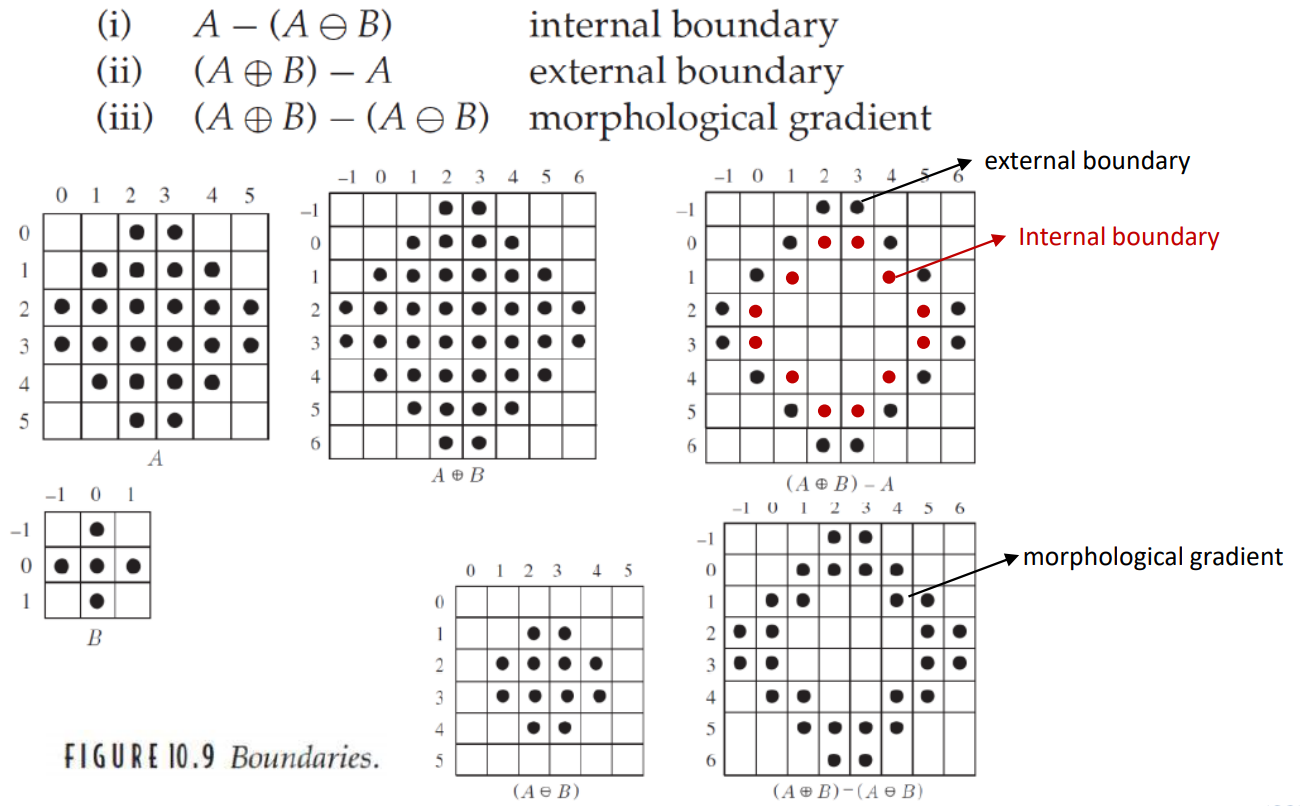
Dilation과 Erosion을 이용하여 Edge detection이 가능하다.
Erosion의 결과는 input image 안에 포함되어 있으므로, input image에서 erosion의 결과를 제거하면 input image에 포함되는 edge가 추출된다.
Dilation의 결과는 input image를 포함하므로, dilation에서 input image를 제거하면 input image를 둘러싸는 바깥의 edge가 추출된다.
두 결과를 합하면 더욱 두꺼운 edge를 추출할 수 있다.

Impulse Noise Removal
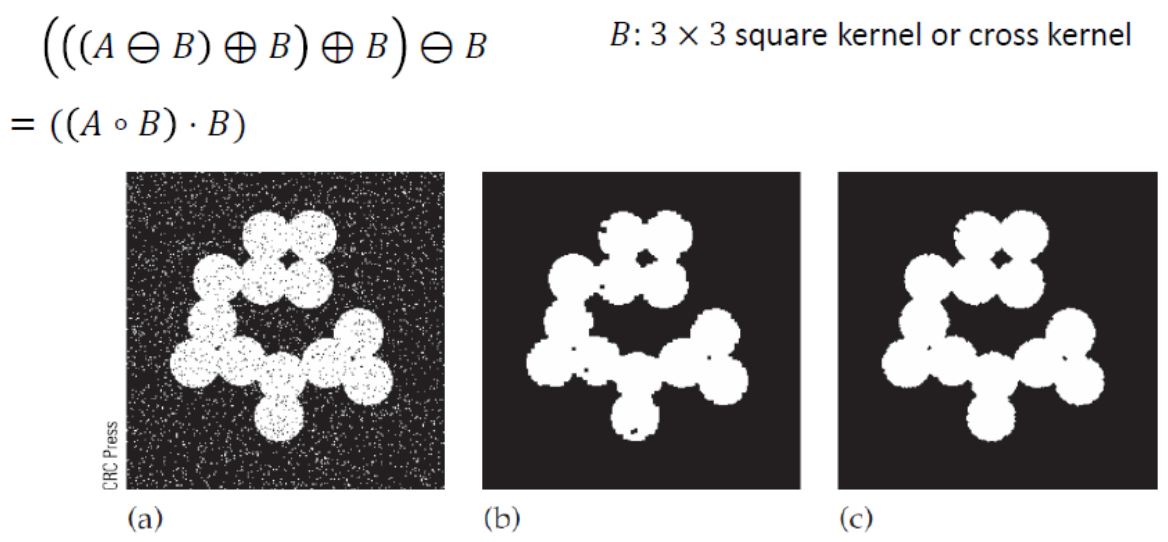
opening후 closing을 하여 noise를 제거할 수 있다.
이미지 a는 기존의 noise 이미지,
b는 8-neighborhood과 자기자신을 black pixel로 설정한 3x3 square kernel을 structing element로 사용했을때,
c는 4-neighborhood과 자기자신을 black pixel로 설정한 3x3 cross kernel을 structing element로 사용했을때를 말한다.



