목차
📁 Edge Detection
이미지의 갑작스러운 불연속적 변화를 식별함으로써 Edge를 감지하고자 한다.
Edge만 나타내도 이미지 대부분의 모양 정보를 알 수 있다.

Edge는 다양한 요소에 의해 결정된다.


하나의 이미지에 위처럼 다양한 Edge가 존재한다.

Edge는 이미지의 intensity function에서 급격한 변화가 나타나는 지점에 존재한다.
intensity는 흑백 이미지에서는 픽셀값이므로, intensity function은 왼쪽 image의 빨간선을 따라서 픽셀을 나열한 함수이고, 이 함수에서 급격한 변화가 나타나는 지점은 곧 픽셀값이 급격하게 변하는 부분이다.
intensity function을 1차 미분하면 edge를 찾는데 유용한 정보를 얻을 수 있다.
오른쪽 1차 미분 함수에서 local minimum과 local maximum, 즉 1차 미분 함수의 extrema(극점)에 edge가 존재한다.

이와 같은 과정으로 미분을 구한다.
맨 아래 수식이 discrete signal을 위한 수식인데, 여기서 나누기 2는 무시해도 된다.
우리가 구하고자 하는 값은 미분 그래프의 극점인데, 수식에 어떤 수를 곱하거나 나눈다고 해서 극점의 위치가 바뀌지 않기 때문이다.
위 미분 수식을 행렬로 나타내면 다음과 같아진다.
[[-1, 0, 1]]
[[-1], [0], [1]]
위 필터는 기본적인 1차 미분 필터이며 첫번째 행렬을 필터형태로 그리면 오른쪽 그림과 같아지는 것이다.
📁 Sobel filter

가운데 세로줄이 0으로 채워진 Soble filter를 보자.
해당 필터가 양 옆으로 픽셀값 차이가 큰 부분에 적용되면, 결과가 큰 값이 나온다.
즉 위 Sobel filter는 vertical(수직적) edge를 감지하는데 효과적이다.
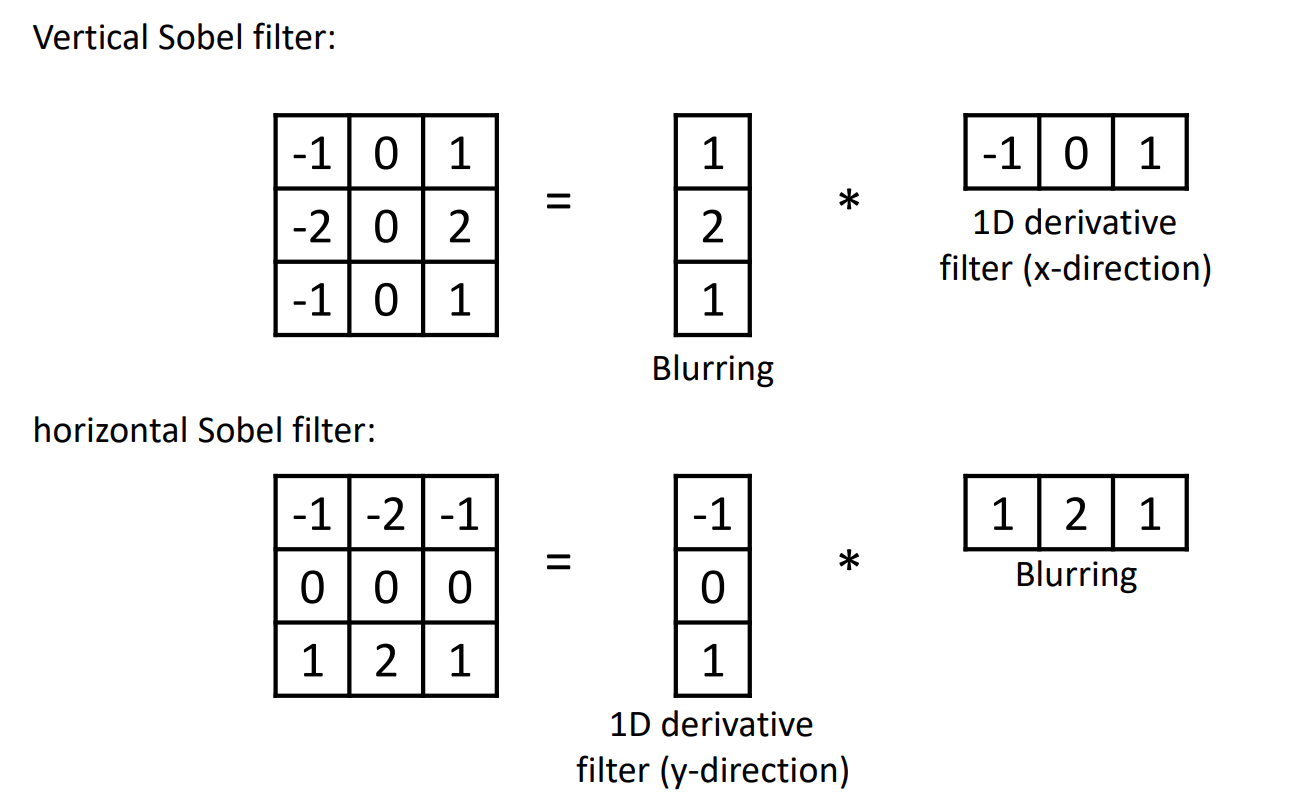
sobel filter는 위에서 구한 1차 미분 행렬을 이용해서 구할 수 있고, vertical과 horizontal 두 가지 버전으로 나눌 수 있다.
vertical sobel filter로 x방향의 변화량을 확인할 수 있으므로, 수직선을 찾을 수 있고
horizontal soble filter로 y방향의 변화량을 확인할 수 있으므로, 수평선을 찾을 수 있다.


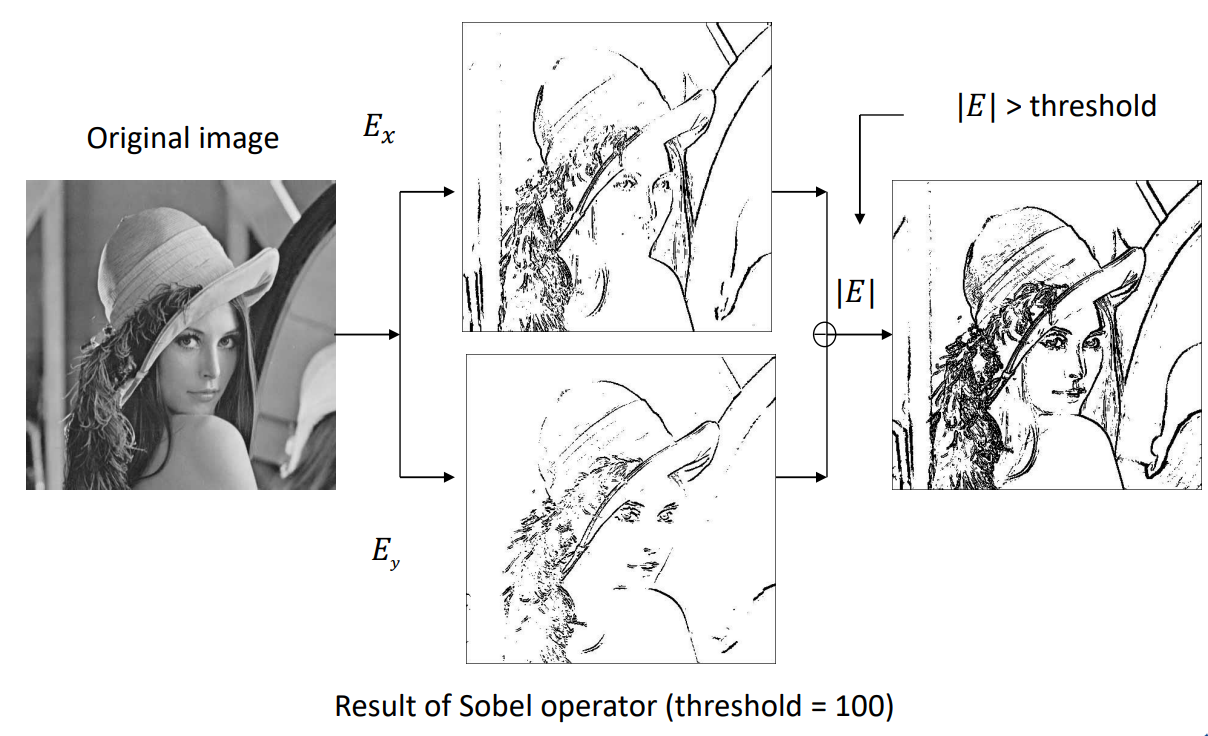
original 이미지에 vertical sobel filter, horizontal sobel filter를 적용한 모습을 보자.
vertical sobel filter를 입힌 모습을 보면 이미지의 수직선들이 강조되어 보이고,
horizontal sobel filter를 입힌 모습을 보면 이미지의 수평선이 강조되어 보인다.
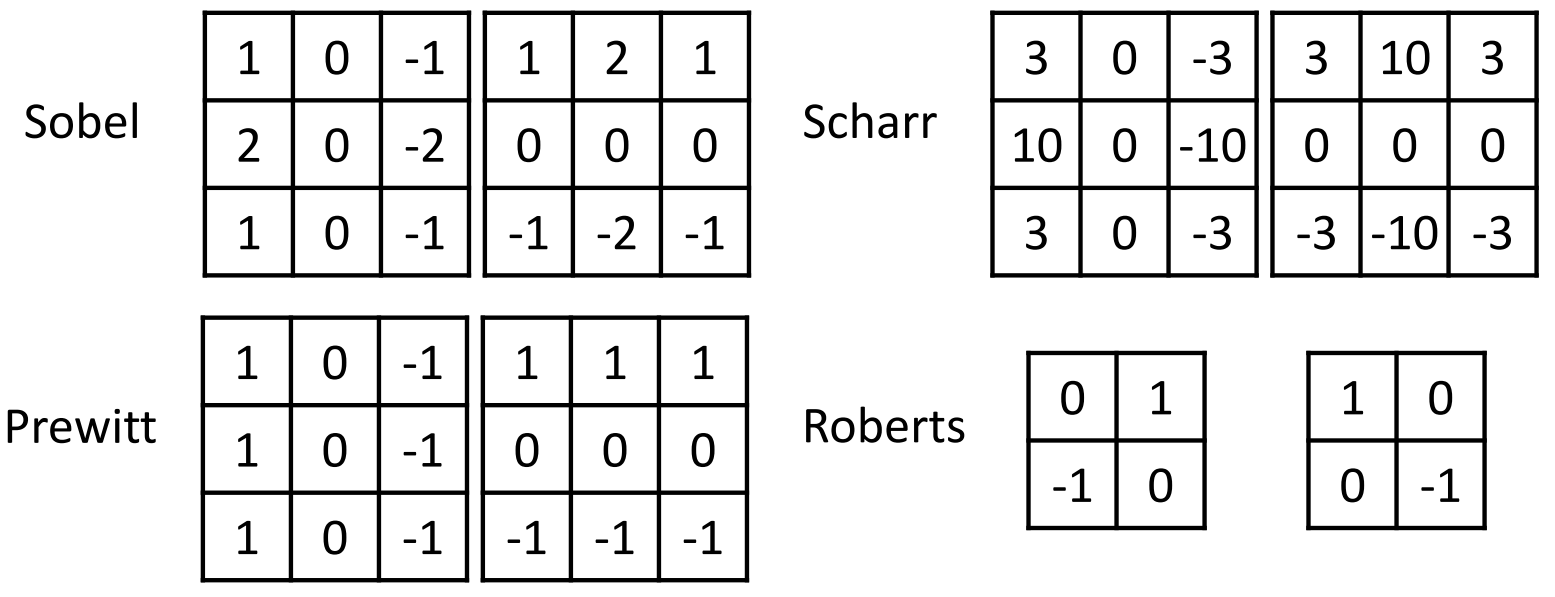
Sobel 필터 외에도 여러가지 미분 필터들이 존재한다.
해당 필터들을 만드는데에는 몇가지 기본 조건이 있다.
1. 피렅의 가로와 세로 크기가 같고 홀수여야한다.
2. 중심을 기준으로 상하좌우가 대칭이어야한다.
3. 모든 수의 합이 0이어야한다.
Roberts 필터는 1, 2번 조건에 해당되지 않아도 된다.
📁 Imgae Gradient
gradient란 변화하는 정도를 나타내는 단어이다.
이미지 내에서는 일반적으로 경계선(edge)에서 큰 변화가 일어나므로, gradient을 계산하여 edge detection에 활용할 수 있다.


📁 Derivative of Gaussian(DoG)
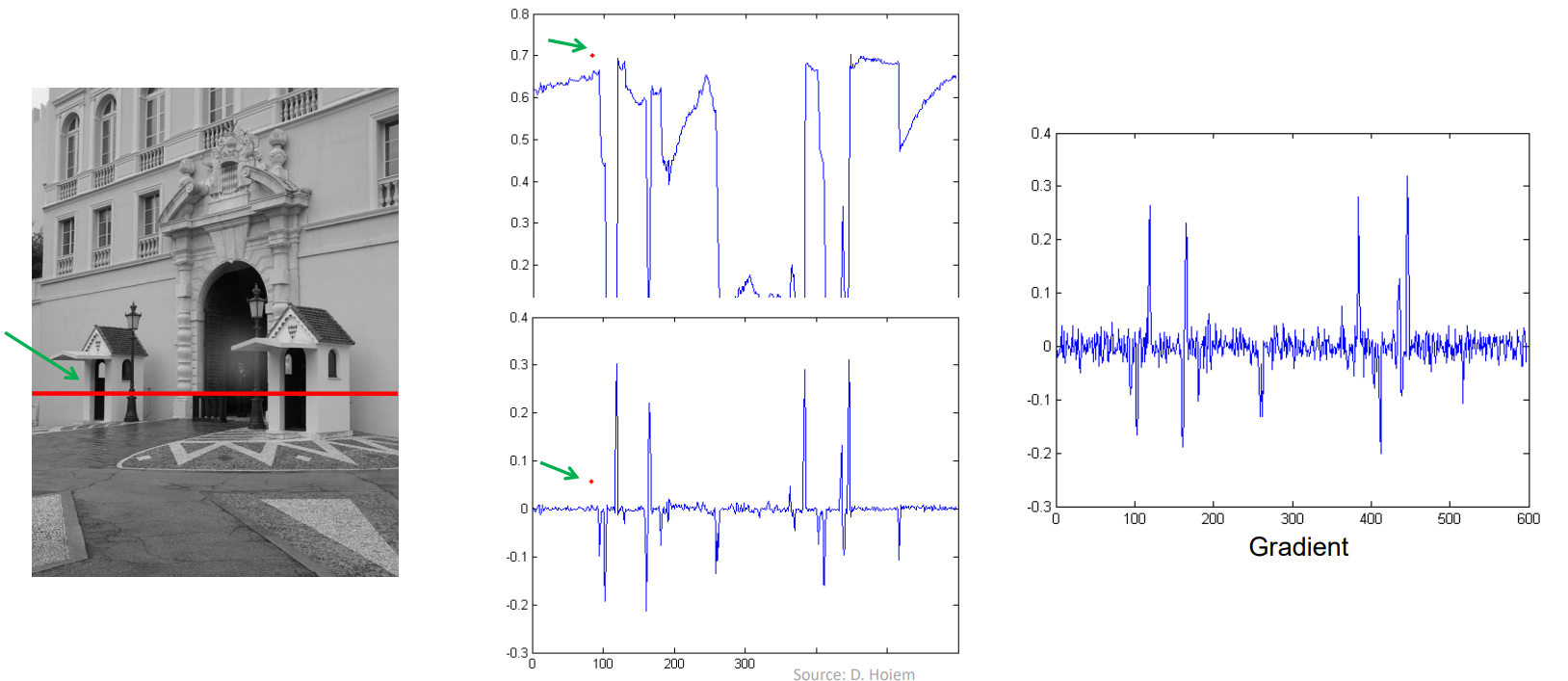
오른쪽 gradient 그래프는 이미지의 빨간선을 따라 각 픽셀간의 변화량 값을 그래프로 나타낸 것이다.
edge가 아닌 부분의 변화량이 0으로 일정하지 않고 여러 값의 gradient가 도출되어 그래프가 작은 지그재그 모양으로 전개되는것을 볼 수 있다.
위 현상은 이미지에 noise가 껴있기 때문이다.
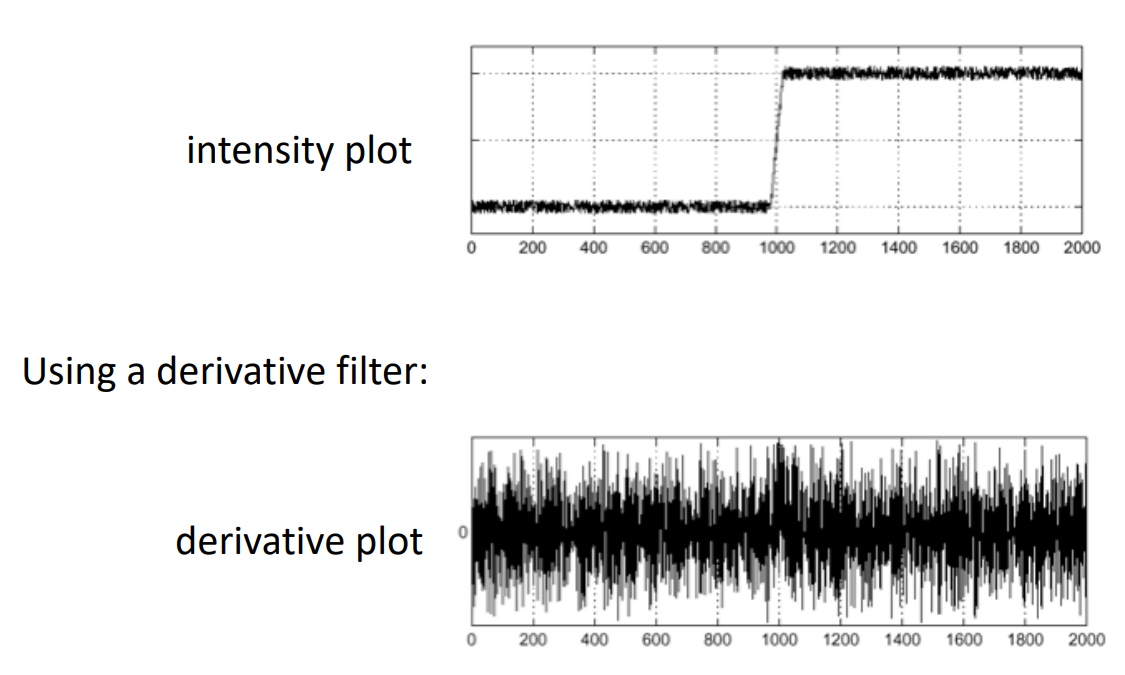
이미지에 noise가 너무 많이 끼면, 아래 derivatie plot 그래프처럼 미분값이 중구난방으로 나오기 때문에 효과적으로 edge를 감지할 수 없다.
위 문제를 해결하기 위해, 이미지에 Gaussian filter를 적용하여 smoothing하는 방법을 적용해볼 수 있다.
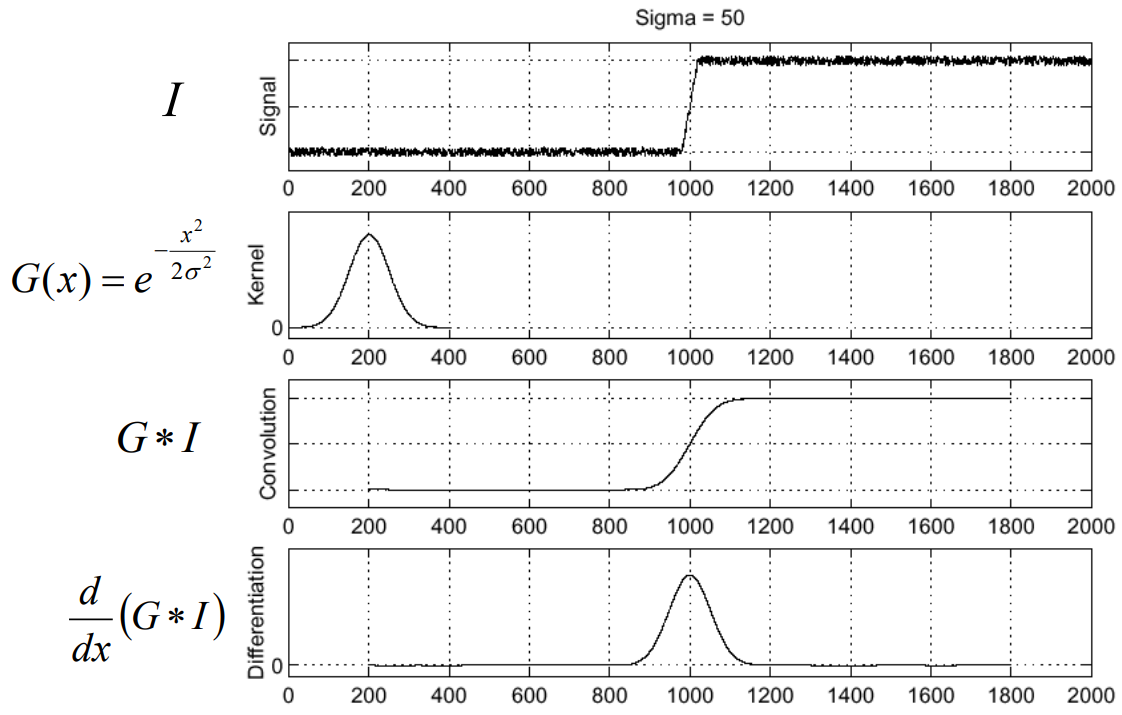
위 그래프들은 이미지에 가우시안 필터를 적용한 후 미분하는 과정을 순서대로 보여준다.
G가 가우시안 필터, I가 이미지를 나타낸다.
첫번째 단계의 I 그래프에서 급격한 픽셀값의 변화를 확인할 수 있는데,
I에 G를 곱한 세번째 단계를 보면 급격한 변화가 있던 지점이 조금 부드러워짐을 확인할 수 있다.
이렇게 되면 edge가 보다 흐려지고 blurring되는 효과가 발생하지만,
앞뒤로 있던 잡음들을 확실하게 없앨 수 있다.
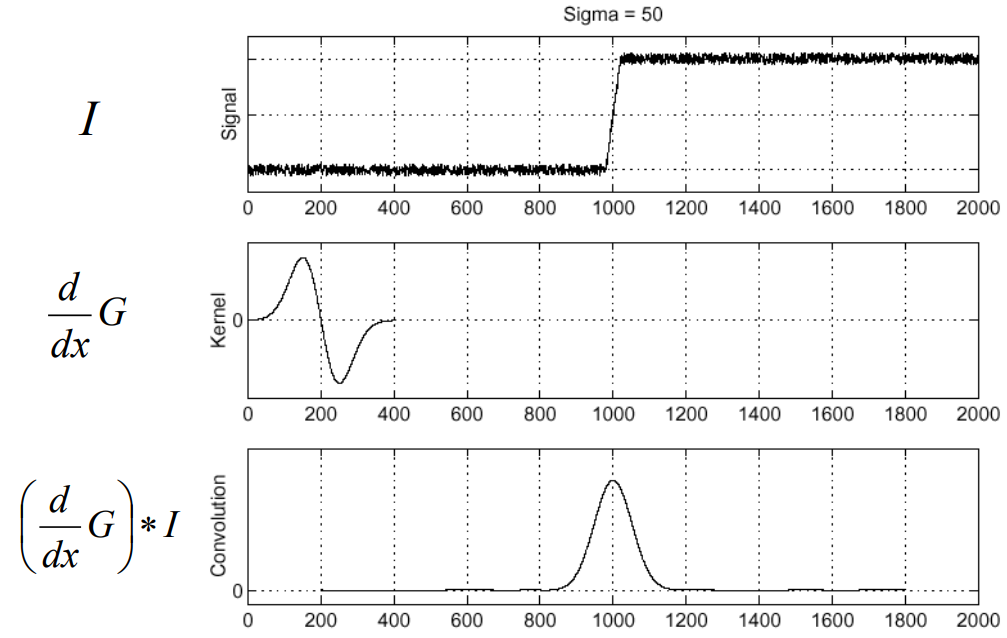
위 4단계를 이처럼 세 단계로 나타낼 수 있다.
4단계에서는 이미지에 가우시안필터를 곱한 후 전체적으로 미분하였지만,
위 그림은 가우시안필터를 먼지 미분한 후 이미지를 곱하였다.
즉 미분의 순서를 바꾸어도 같은 결과가 나오면서, G를 곱하는 연산을 없앰으로써 연산량을 줄일 수 있다.
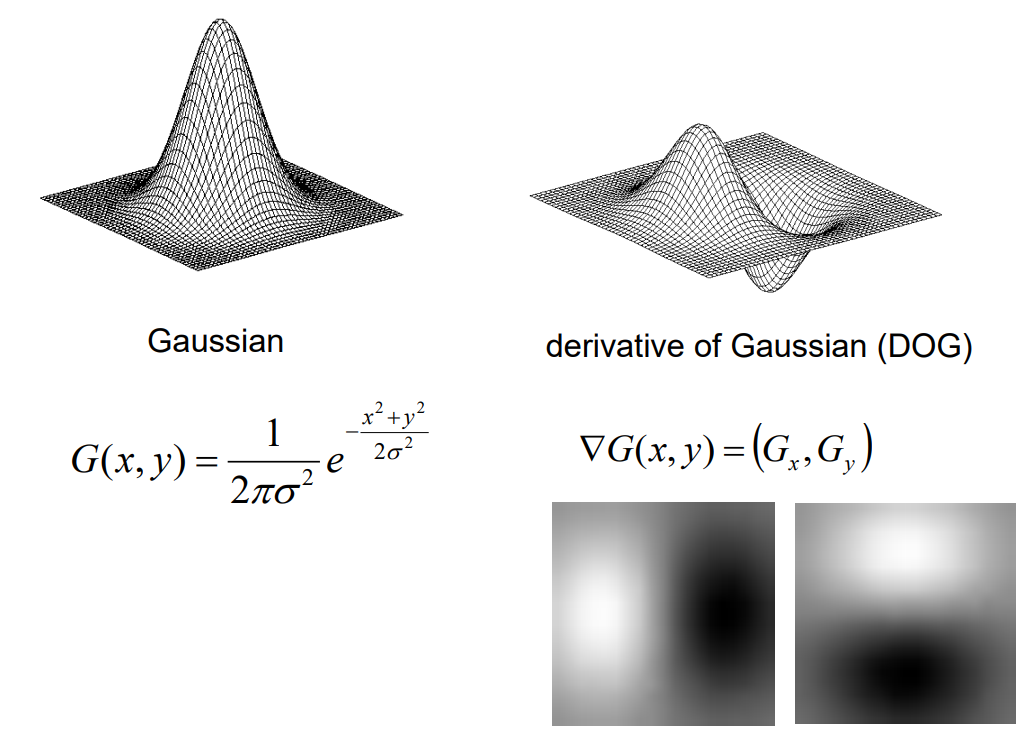
이와 같이 가우시안 필터에 미분을 적용한 필터를 Derivative of Gaussian(DOG)라고 칭한다.
📁 Laplace filter



