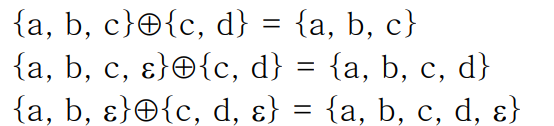LL파싱은 결정적 파싱이 되는 문법을 선별하여, 각 입력 문자당 적용될 생성규칙을 미리 뽑아두고 시작한다.
이를 위해 규칙으로부터 필요한 정보들에는 FIRST 집합이 있다.
📁 FIRST

FIRST란 Nonterminal A로부터 유도되어 첫번째로 나타날 수 있는 terminal들의 집합을 말한다.
예를 들어, 다음 문법의 FIRST(S), FIRST(A), FIRST(B)는 다음과 같다.


📁 FIRST(X)를 계산하는 방법
정의 1. X가 terminal이면 FIRST(X)는 자기 자신이 된다.

이때 X는 Nonterminal이어야하지만, 위 규칙은 계산의 편의를 위해 확장한 개념이다.
정의 2. X-> aα 와 같이 맨 처음이 terminal인 생성규칙이 존재하면 해당 terminal a가 FIRST(X)에 포함된다.

정의 3. X -> ε와 같이 X가 null생성규칙을 가지는 경우 FIRST(X)에 ε이 포함된다.

정의 4. X -> Y1Y2Y3..Yk인 생성규칙이 있을 때, FIRST(X)는 FIRST(X)와 FIRST(Y1Y2,...Yk)의 합집합이다.


위 정의를 기반으로, 아래 과정을 따라 FIRST 집합을 계산할 수 있다.
- 초기에, 모든 Nonterminal의 FIRST는 공집합으로 시작한다.
- RHS에 첫번째로 terminal이 나오는 생성규칙(null생성규칙 포함)에서 먼저 FIRST를 구한 후, 이 형태의 생성규칙은 다시 고려할 필요가 없기 때문에 제거한다.
- 남은 생성규칙의 RHS는 모두 Nonterminal로 시작하므로, Ringsum 연산을 이용해 모든 Nonterminal의 FIRST가 변하지 않을 때 까지 반복한다.
참고로, 일반적으로 A의 생성 규칙이 A->a | b | c | ... | z와 같은 형태일 때, FIRST(A)는 다음과 같이 계산된다.

예를 들어 다음과 같은 문법이 주어졌을때, FIRST(S), FIRST(A), FIRST(B)를 구해보자.

먼저 FIRST(S), FIRST(A), FIRST(B) 모두 {}, 공집합으로 시작한다.
다음으로 RHS에 terminal이 먼저 나오는 경우를 찾아보면
A -> dB | aS | c
B -> b
해당 규칙들을 찾을 수 있다.
위 규칙들에 대해 FIRST의 정의 중 (1), (2), (3) 을 따라 FIRST를 구하면 아래와 같다.
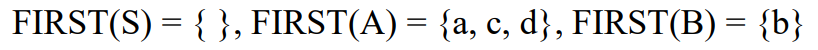
위 규칙들은 더이상 고려할 필요가 없으므로 제거하면 남은 규칙들은
S -> ABe
B -> AS 와 같다.
위 규칙들에 대해 FIRST 정의 (4)를 따라 계산하면 아래와 같다.
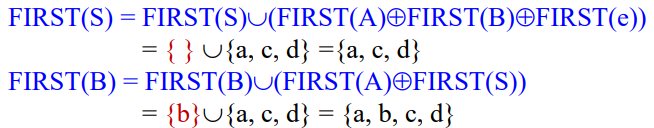
위 과정으로 계산한 결과 FIRST(S) = {a, c, d}, FIRST(B) = {a, b, c, d}가 도출되었는데,
최종 결과를 도출하기 위해서는 이렇게 도출된 결과를 위 계산에 적용시켜서 한번 더 반복해야한다.
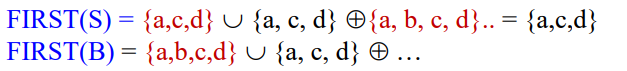
반복하여 계산한 결과 이전의 결과와 같으면, 해당 결과가 최종이 된다.
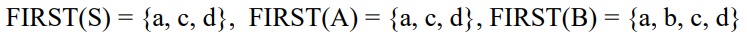
🌱 ε-생성규칙(null 생성규칙)
ε -생성규칙이란 아래와 같은 형태의 생성규칙을 말한다.
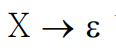
Nonterminal A가 ε을 유도할 수 있으면 A를 nullable nonterminal이라고 부른다.
즉, A부터 전개되는 유도과정 안에 null생성규칙이 존재하면 nullable한것이다.
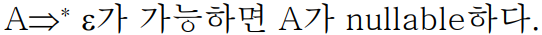
🌱 LHS, RHS
생성규칙 A -> XXX에서,
LHS(Left Hand Side) : A
RHS(Right Hand Side) : XXX
🌱 ⊕ (Ringsum)
ringsum ⊕은 두 개의 집합에 대한 연산자로, 다음과 같이 정의된다.
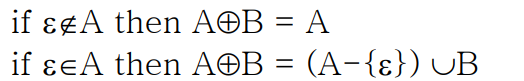
A에 ε이 없는 경우 ringsum의 결과는 A이고,
A에 ε이 있는 경우 ringsum의 결과는 A에서 ε을 제외한 나머지와 B의 합집합이다.
예를 들면 다음과 같다.