[PL] Conditional Branch

📁 Conditional Branch

특정 조건에 따라 서로 다른 행동을 수행하는 구문을 conditional branch라고 한다.

조건을 만족하는 경우 true branch, 만족하지 않는 경우 false branch를 수행하는 방식이다.

 

일반적으로 if-else 혹은 if-then-else의 형태를 띄는데, 삼항연산자(e1 ? e2 : e3) 등 그 외의 형태도 존재한다.

 

 

 

 

📁 Extension of FVAE: CFVAE

해당 포스팅에서는 FVAE에 조건분기문을 추가한 CFVAE(Conditional branch and FVAE)를 정의한다.

 

CFVAE언어는 다음과 같이 정의된다.

 

F1VAE 언어의 예시는 다음과 같다.

 

 

 

 

📁 CFVAE의 Concrete syntax

FVAE는 하나의 표현식으로 이루어진 프로그램이다.

가장 상단의 expr은 이를 의미한다.

 

# if expr1 then expr2 else expr3는 조건분기문을 정의하는 concrete syntax이다.

• expr1 : 조건 expression
• expr2 : true branch expression
• expr3 : false brnach expression

 

# expr1 < expr2는 크기 비교 연산을 정의하는 concrete syntax이다.

 

# bool은 true 혹은 false의 논리값을 나타내는 concrete syntax이다.

 

 

 

 

 

 

 

📁 CFVAE의 Abstract syntax

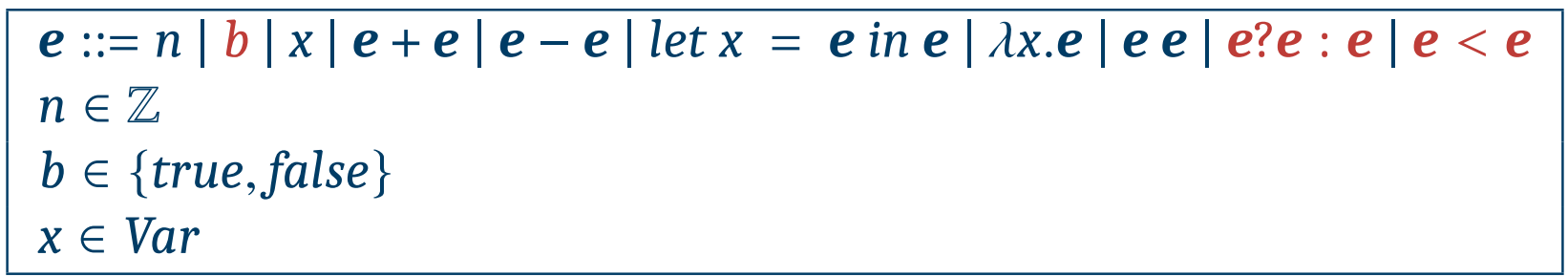
빨간 글씨가 CFVAE에 새로 추가된 Abstract syntax이다.

 

 

 

b

true 혹은 false 값을 나타내는 abstract syntax이다.

 

b는 아래 트리를 나타내는 축약 코드이다.

b가 true 혹은 false 값을 나타낼 경우, 오른쪽과 같은 트리가 Expr 집합에 속함을 의미한다.

 

위 트리에서 Bool은 아래 Value Domain에서 새로 정의되는 domain에 추가된 Bool과 같다.

즉 abstract syntax에서 쓰이는 value들이 value domain에 포함된다.

 

 

 

e1 ? e2 : e3

조건분기문을 나타내는 abstract syntax이다.

 

e1은 조건문 (condition expression)이고,

e2는 true branch expression, 즉 조건문이 true인경우 수행하는 expression이고,

e3은 false branch expression, 즉 조건문이 false인 경우 수행하는 expression이다.

 

 

e ? e : e는 아래 트리를 나타내는 축약코드이다.

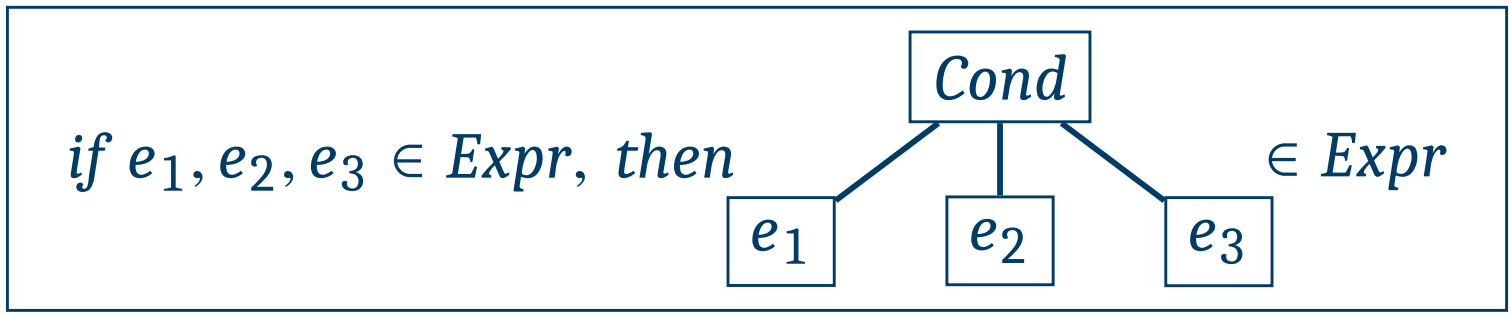
e1, e2, e3이 Expr 집합에 속할 때, 오른쪽같은 트리가 Expr 집합에 속함을 의미한다.

 

 

 

e1 < e2

Less-than expression을 나타내는 abstract syntax이다.

 

e1은 LHS expressoin, 즉 비교문에서 왼쪽에 자리한 좌항 exprssion이고,

e2는 RHS expression, 즉 비교문에서 오른쪽에 자리한 우항 exprssion이다.

 

 

e 1< e2는 아래 트리를 나타내는 축약코드이다.

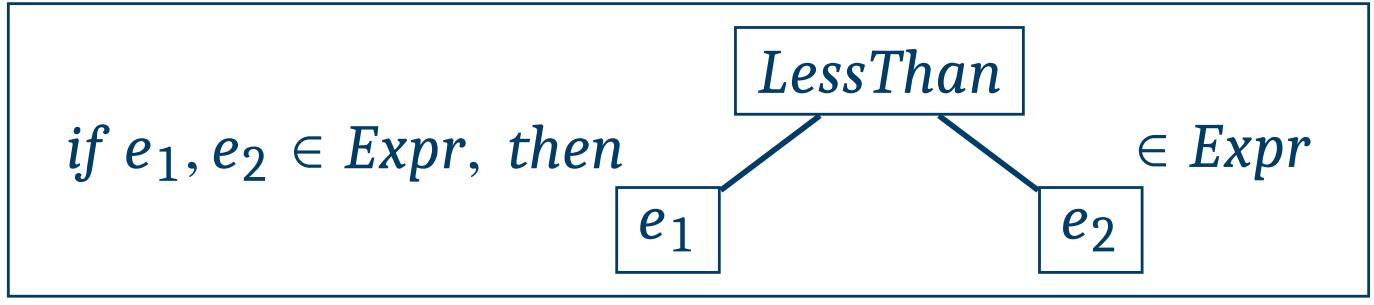
e1와 e2가 Expr 집합에 속할 경우, 오른쪽같은 트리가 Expr 집합에 속함을 의미한다.

 

 

 

🔎 OCaml 구현

type expr =
    | Num of int
    | Bool of bool
    | Id of string
    | Add of expr * expr
    | Sub of expr * expr
    | LetIn of string * expr * expr
    | App of expr * expr
    | Lambda of string * expr
    | Cond of expr * expr * expr
    | LessThan of expr * expr

 

 

 

 

📁 Value Domain in CFVAE

CFVAE는 true와 false라는 값을 지원하므로, "값"의 확장이 요구된다.

 

이전의 FVAE에서 boolean값을 나타내는 Bool을 추가하여 이와 같이 수정한다.

 

 

 

🔎 OCaml 구현

type value =
    | NumV of int
    | ClosureV of string * Ast.expr * t
    | BoolV of bool

Ocaml에서 boolean값을 bool로 표현한다.

 

 

 

📁 CFVAE의 Semantics

Semantics

 

 

 

Formal Semantics

 

 

 

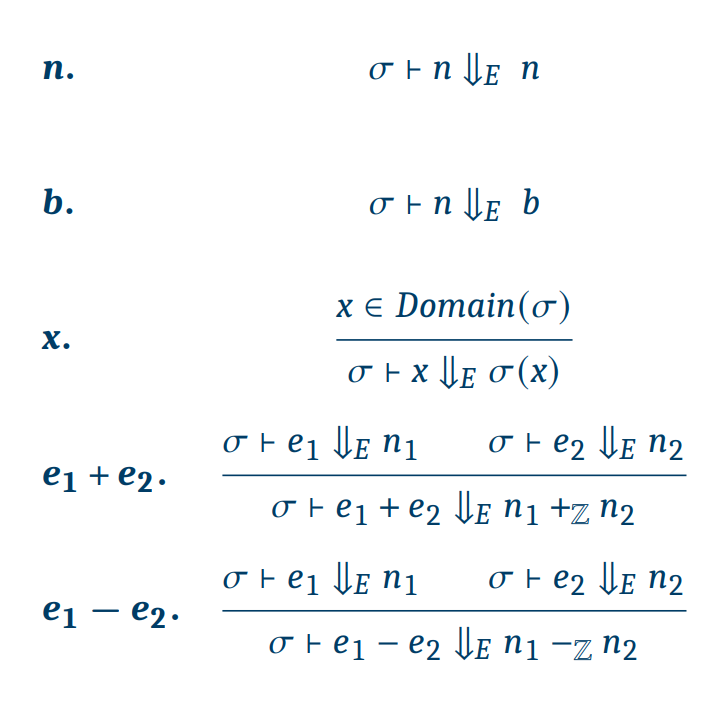
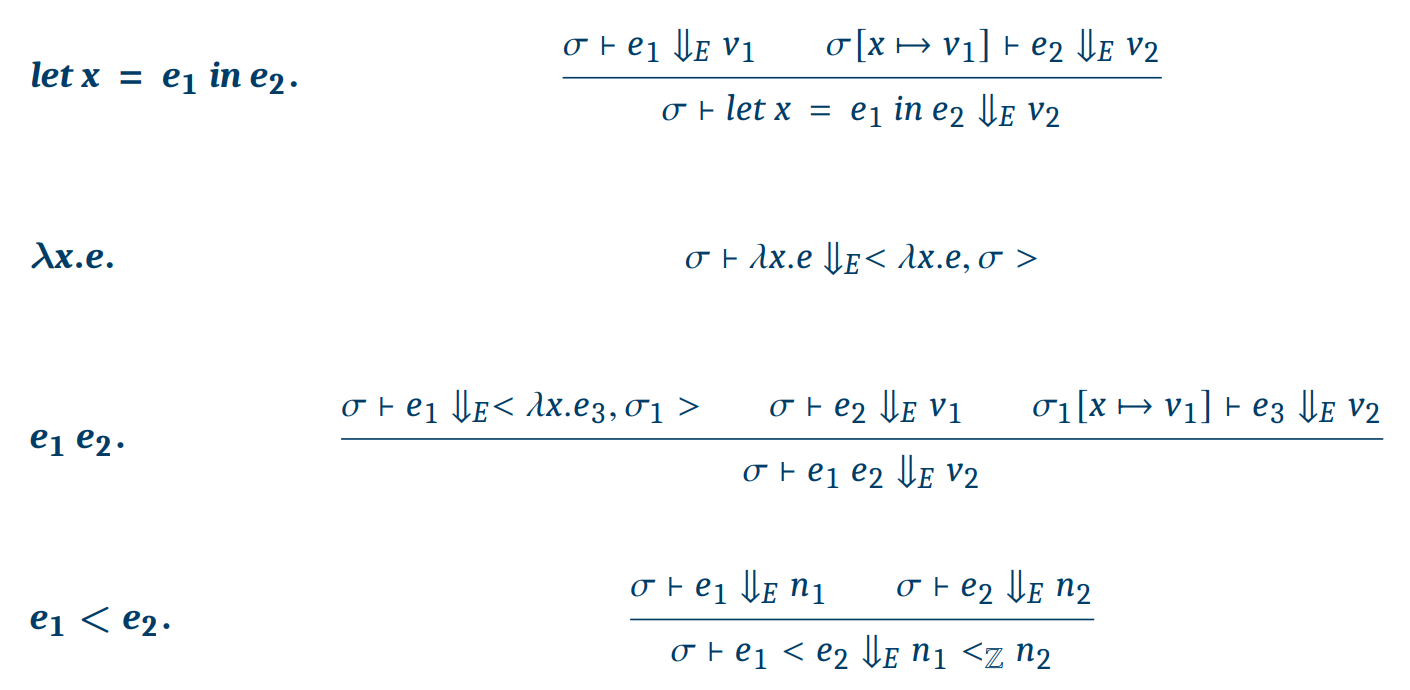
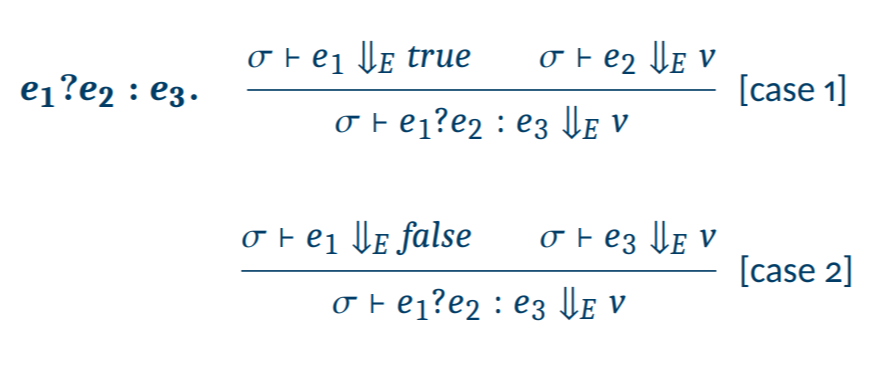
📁 Example of CFVAE

true (* true *)
false (* false *)
1 < 3 (* true *)
3 < 2 (* false *)
1 < (0 + 1) (* false *)
(1 - 1) < (0 + 1) (* true *)
(1 - 1) < true (* runtime error *)
if true then 1 else 3 (* 1 *)
if false then 1 else 3 (* 3 *)
if (1 - 1) < (0 + 1) then 0 + 7 else 3 (* 7 *)
if (1 + 0) then 0 + 7 else 3 (* runtime error *)

 

 

 

 

📁 Syntactic Sugar를 이용한 boolean값 확장

true와 false, 즉 boolean 값을 지원하는 CFVAE는 Value Domain이 복잡해진다.

 

이를 Syntactic sugar 방법을 이용해 간단하게 확장하는 방법이 있는데, 두가지 옵션이 존재한다.

 

이때 true와 false는 "기존의 값"으로 표현하므로, Value Domain은 FVAE에서 변경 없이 그대로 사용한다.

 

 

 

 

Option1. C style

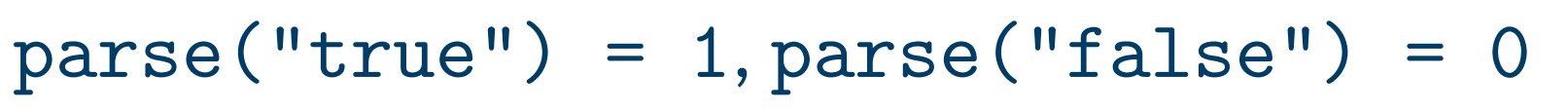
true와 false를 정수로 표현하는 방법이다.

 

concrete syntax에는 syntactic sugar이므로 true 혹은 false를 표현하는 b가 그대로 남아있되, 이를 1 또는 0 정수값으로 파싱하는 것이다.

 

 

 

Abstract Syntax

 

 

 

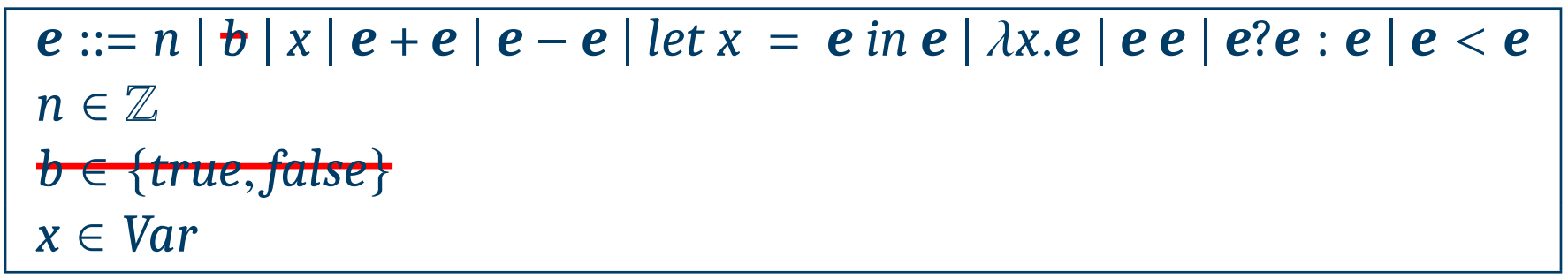
Semantics 및 Formal Semantics

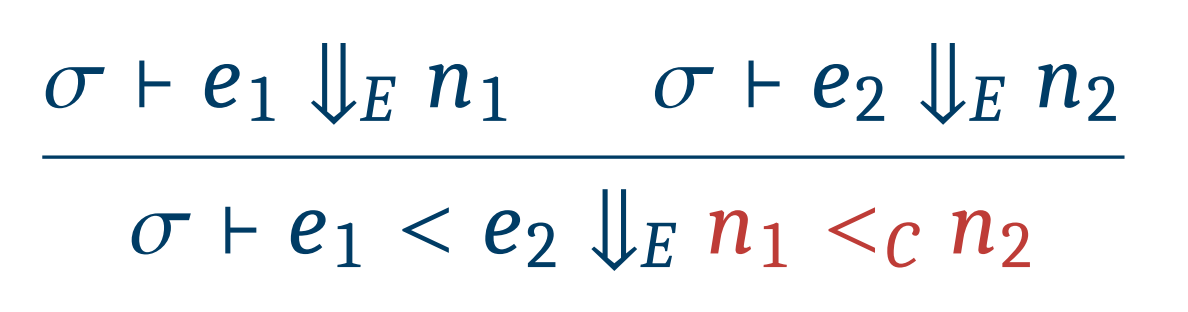
e < e에 대한 Semantics는 이와 같이 정의된다.

 

기존의 Semantics와의 차이점은, 비교 연산자가 <D에서 <C가 되었다는 점이다.

 

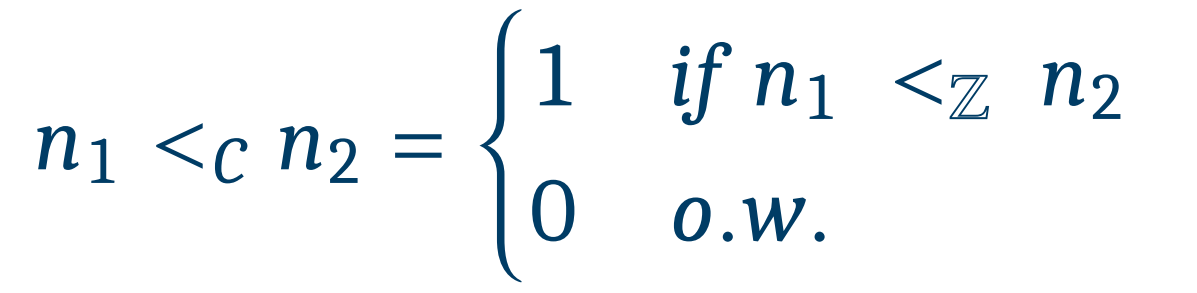
<C의 정의이다.

 

 

 

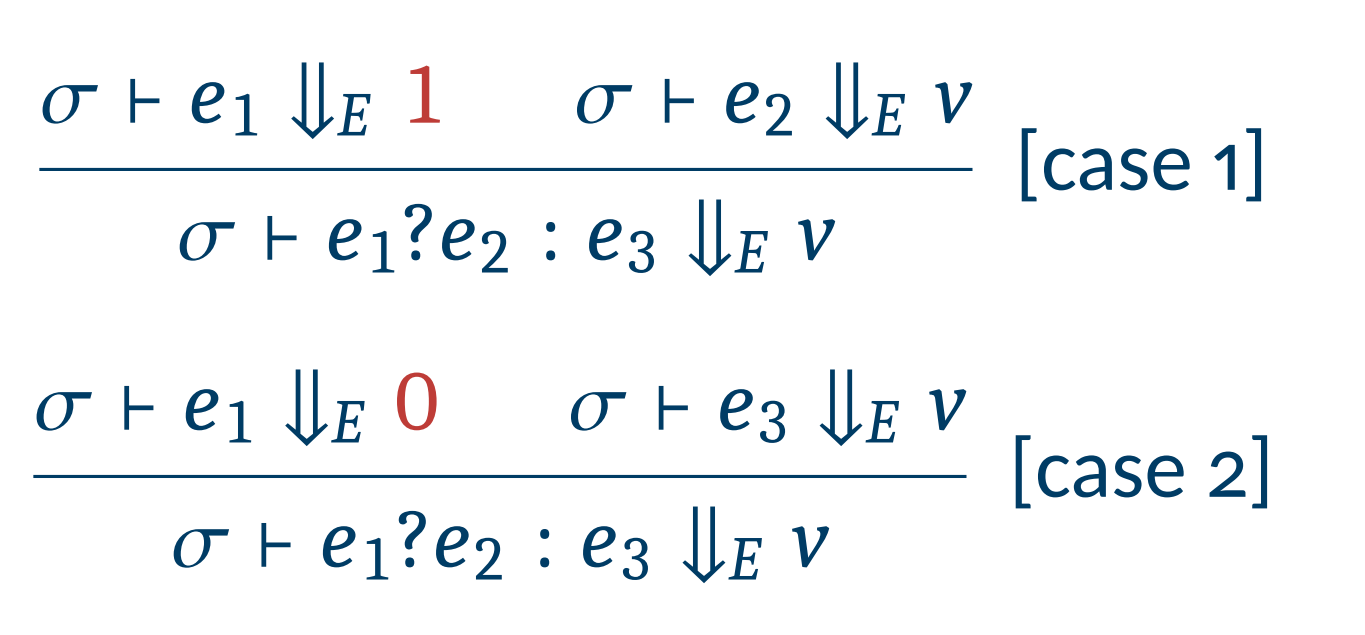
e ? e : e에 대한 Semantics는 이와 같이 정의된다.

 

기존의 semantics에는 위 빨간글씨로 표시된 1과 0이 true와 false값이었다.

 

 

 

Examples

true (* 1 *)
false (* 0 *)
1 < 3 (* 1 *)
3 < 2 (* 0 *)
1 < (0 + 1) (* 0 *)
(1 - 1) < (0 + 1) (* 1 *)
(1 - 1) < true (* 1 *)
if true then 1 else 3 (* 1 *)
if false then 1 else 3 (* 3 *)
if (1 - 1) < (0 + 1) then 0 + 7 else 3 (* 7 *)
if (1 + 0) then 0 + 7 else 3 (* 7 *)
if (1 + 2) then 0 + 7 else 3 (* runtime error *)

 

 

이를 더 general하게 표현하면 e? e : e의 Semantics를 다음과 같이 수정할 수 있다.

 

 

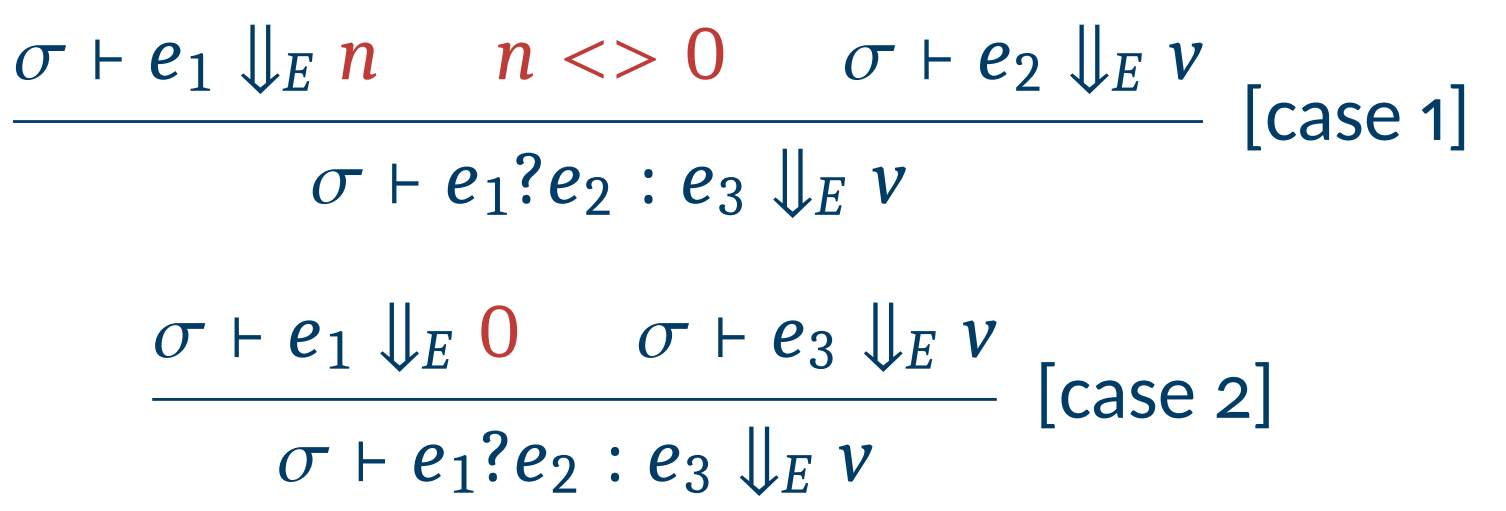
위 semantics를 적용하면 위 예시는 다음과 같이 결과값이 바뀐다.

true (* 1 *)
false (* 0 *)
1 < 3 (* 1 *)
3 < 2 (* 0 *)
1 < (0 + 1) (* 0 *)
(1 - 1) < (0 + 1) (* 1 *)
(1 - 1) < true (* 1 *)
if true then 1 else 3 (* 1 *)
if false then 1 else 3 (* 3 *)
if (1 - 1) < (0 + 1) then 0 + 7 else 3 (* 7 *)

 

 

 

 

Option2. Church boolean

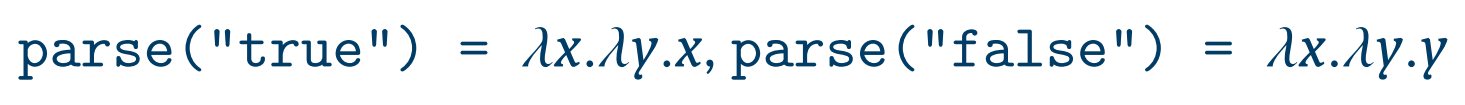
true와 false를 closure로 표현하는 방법이다.

 

마찬가지로 concrete syntax에는 syntactic sugar이므로 true 혹은 false를 표현하는 b가 그대로 남아있되, 이를 위와같은 closure로 파싱하는 것이다.

 

Church encoding은 데이터 및 데이터 간의 연산을 lambda calculus로 나타내기 위한 encoding이다.

 

즉 모든 데이터와 데이터간의 연산을 lambda abstraction과 application으로 표현한다.

 

true 값은 𝜆x.𝜆y.x로, false 값은 𝜆x.𝜆y.y로 표현하는데, 이는 lambda abstraction을 이용한 표현법이다.

e1? e2 : e3을 e1 e2 e3으로 표현하는데, 이는 application을 이용한 표현법이다.

 

 

즉 위 표현법들을 적용하면 두 branch에 따라 e1? e2 : e3의 표현법을 위와 같이 변형시킬 수 있다.

 

 

 

Abstract Syntax

 

 

 

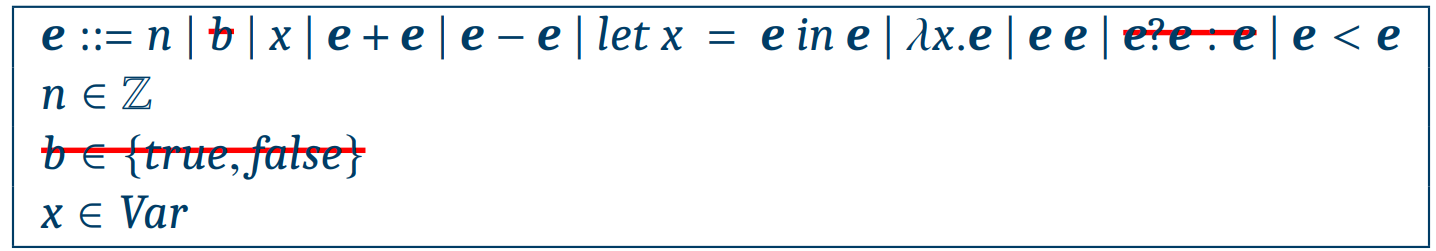
Semantics and Formal Semantics

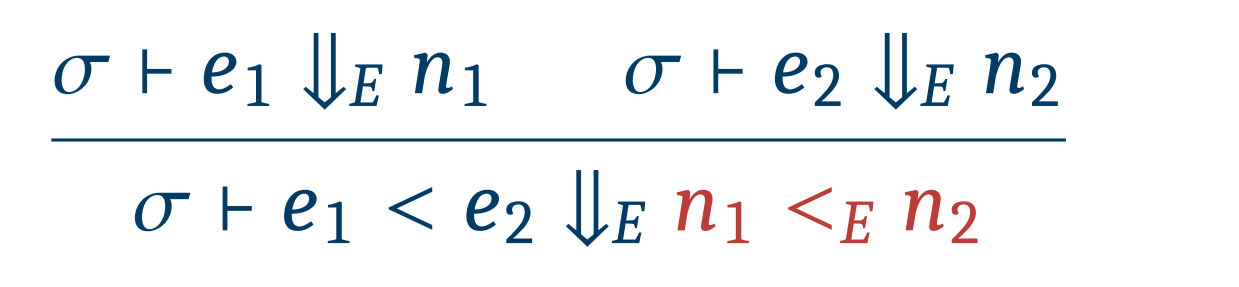
e < e에 대한 Semantics는 이와 같이 정의된다.

 

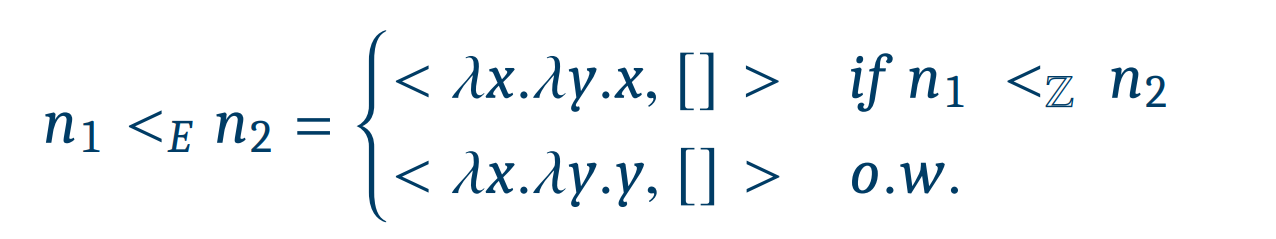
<E는 이와 같이 정의된다.

 

 

 

Example

true (* < 𝜆x.𝜆y.x, [] > *)
false (* < 𝜆x.𝜆y.y, [] > *)
1 < 3 (* < 𝜆x.𝜆y.x, [] > *)
3 < 2 (* < 𝜆x.𝜆y.y, [] > *)
1 < (0 + 1) (* < 𝜆x.𝜆y.y, [] > *)
(1 - 1) < (0 + 1) (* < 𝜆x.𝜆y.x, [] > *)
(1 - 1) < true (* runtime error *)
if true then 1 else 3 (* 1 *)
if false then 1 else 3 (* 3 *)
if (1 - 1) < (0 + 1) then 0 + 7 else 3 (* 7 *)
if (1 + 0) then 0 + 7 else 3 (* runtime error *)
(1 > 3) (0 + 7) 3 (* 3 *)
(1 + 3) (0 + 7) 3 (* runtime error *)