목차
📁 Simple programming language를 정의하기 위해 필요한 두 가지 정의
Syntax 정의
syntax를 정의하는 방법에는 concrete syntax와 abstract syntax 두 가지가 있다.
Concrete syntax는 언어의 실제 문법적인 표현이다. 개발자들이 사용하는 문법이다.
Abstract syntax는 back-end에서 사용하기 좋게 정리된 문법이다.
Semantics 정의
semantics에 기반하여 프로그램의 실행 결과를 증명할 것이다.
semantics는 자연어로 혹은 수학적으로 엄밀하게 정의할 수 있다.
📁 AE : Arithmetic Expression
Arithmetic Expression은 본 포스팅에서 정의할 간단한 형태의 프로그래밍 언어이다.
AE의 구성 요소는 다음과 같다.

이때 특정 문법에 속한 모든 문자열의 집합이 곧 언어이므로,
L(GAE)는 정수 사이의 덧셈과 뺄셈으로 이루어진 언어라고도 말할 수 있다.
📁 Concrete syntax of AE
아래 예시들은 Concrete syntax를 BNF로 나타낸 것이다.
1. Numbers에 대한 Concrete syntax

위 syntax의 각 요소는 다음과 같이 정의된다.



최종적으로 산출되는 number는 정수를 나타내는 문자열의 집합이다.
2. Expression에 대한 Concrete syntax

위 syntax의 요소는 다음과 같이 정의된다.

최종적으로 산출되는 expr는 정수간의 덧셈 및 뺄셈으로 이루어진 표현식을 나타내는 문자열의 집합이다.
위 syntax는 ambiguous grammar이지만, 본 포스팅에서는 설명의 편의를 위해 무시하도록 한다.
📁 Abstract syntax
📌 Abstract syntax란 프로그램을 나타내는 tree형태의 구문구조이다.
각 프로그램은 여러개의 구문으로 구성되어있고, 각 구문은 세부구문으로 구성되어있다.
예를 들면 expr이 expr, +, expr로 구성되어있는 것과 같다.
Tree의 재귀적 구조를 활용하면 위와 같은 특성을 가지고 있는 프로그램을 표현하기에 용이하다.
구문-세부구문의 관계를 tree 내의 tree-subtree 혹은 부모-자식 관계로 재귀적으로 구성이 가능하다.
다음은 abstract syntax를 정의하는 예시이다.

위 예시는 네가지 언어로 쓰인 서로 다른 concrete syntax들이며, 모두 같은 semantics를 가진다.
이를 abstract syntax로 정의하면 다음과 같이 동일한 트리형태가 나온다.


abstract syntax는 프로그램에서 불필요한 문법적 디테일을 제거하는 과정을 거치기 때문에,
위 트리에서 아래 트리로 완성되는 과정에서 Var 부분이 사라지는 것을 확인할 수 있다.
🔎 abstract syntax를 정의하는 이유
위에서 언급했듯이, abstract syntax는 concrete syntax에서 불필요한 문법적 디테일을 제거한다.
예를 들어 두 정수의 합을 계산하는 AE의 concrete syntax를 살펴보자.
-2와 0 - 2는 서로 다른 concrete syntax이지만,
두 표현식은 모두 개발자가 작성 가능한 유효한 표현식이고, 두 표현식을 구분지을 필요가 없다.
Abstract syntax에서는 두 표현식을 모두 0 - 2라고 표현할 수 있다.
만약 2 + 1과 2 - 1을 비교해보자. 둘은 서로 다른 concrete syntax이다.
두 표현식 모두 유효하고, 의미가 다르므로 구분지을 필요 또한 있다.
이와 같은 경우 Abstract sytnax에서도 둘을 구분지어 각각 2 + 1과 2 - 1로 표현한다.
📁 Abstact syntax of AE
Abstract syntax는 프로그램을 tree구조로 표현하며, 그렇게 표현된 모든 tree의 집합을 뜻한다.
다음은 AE의 abstract syntax를 집합 Expr로 표현한다.
1. Number에 대한 abstract syntax

Num은 AE의 정수를 표현하는 노드이며, Z는 정수의 집합이다.
2. Addition에 대한 abstract syntax

Add는 AE의 덧셈을 표현하는 노드이다.
덧셈 연산에 필요한 두개의 operand 자식 노드를 가지고 있으며, 두 자식노드 역시 집합 Expr의 원소이다.
3. Subtraction에 대한 abstract syntax

Sub는 AE의 덧셈을 표현하는 노드이다.
뺄셈 연산에 필요한 두개의 operand 자식 노드를 가지고 있으며, 두 자식노드 역시 집합 Expr의 원소이다.
🔎 Abstract syntax in OCaml
🔎 Code-like description of abstract syntax
Abstract syntax는 tree형태로 구성되는데, 이는 주로 축약된 코드 형태로 기술될 수 있다.

위와 같이 축약된 코드 형태를 이용하여 다음과 같은 abstract syntax를 새롭게 정의할 수 있다.

위 정의를 간단하게 BNF로 정의하면 다음과 같다.

위 abstract syntax에서 n과 e는 치환될 수 있는 것들(metavariable)이다.
실제 프로그래밍 언어의 변수가 아닌, 고차원적인 변수라는 뜻이다.
n은 하나의 정수를 나타내는 변수이며, e는 하나의 AE expression을 나타내는 변수이다.
위 BNF를 Concrete syntax와 비교해보면,
예시에 볼 수 있듯이 -2와 0 - 2를 구분하지 않고 모두 0 - 2라고 표현하므로,
abstract syntax에서는 음수가 없다고 가정함으로써 불필요한 문법적 디테일을 제거하여 두번째 줄과 같이 표현할 수 있다.
여기서 주의할점은, Abstract syntax의 +와 -는 수학 연산자가 아니다.
syntax이기 때문에 덧셈 및 뺄셈에 대한 의미가 주어지지 않았으므로, 단지 Add와 Sub에 대한 syntax를 코드 형식으로 표현한 것 뿐이다.
본 포스팅에서는 Expr 도메인의 연산기호를 +, -로, 정수 도메인의 연산기호를 +z, -z로 표현한다.
🔎 Parsing AE program to AST
파싱을 통해 AE 프로그램을 AST로 변환한다.

📁 Sementics of AE
🔎 프로그래밍언어의 semantics와 프로그램의 semantics
아래 세 단계는 formal semantics에 가까워지는 과정이다.
1. 자연어로 기술한 Semantics of AE
2. Binary realation으로 정의한 Sematics of AE
3. Inference rule을 이용한 Semantics of AE
📌 Inference rule(추론 규칙)이란 전제로부터 결론을 이끌어내는 규칙을 말한다.
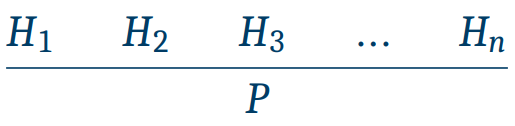
- H1, H2, H3, ..., Hn : premises(전제)
- P : conclusion(결론)
- Premises : H1, H2, H3, ..., Hn 가 모두 참이면, conclusion P는 참이다.
📁 Proof tree
📌 Proof tree란 Inference rule을 이용하여 결론을 증명하는 과정을 나타내는 tree 형태의 자료구조를 말한다.
proof tree의 root는 conclusion(결론)을 의미하므로, 일반적인 tree와 달리 root가 가장 아래에 위치해있다.
자식 노드는 부모 노드에 대한 증거로서, 자식 노드가 모두 참인 경우 부모 노드도 참이다.
Operational semantics를 활용하여 프로그램을 대상으로 proof tree를 그려 실행하고 결과를 유추 및 증명한다.
📝 예시
다음은 (3 - 1) + 2가 4로 계산됨을 증명하는 proof tree이다.

proof tree의 리프노드는 모두 엑시움(전제가 필요없는 명제)이어야한다.



